1.
Einleitung ^
Anlass zum vorliegenden Beitrag geben vor allem Entscheidungen des BVerfG zu Fragen der juristischen Methodenlehre und den Rechtsprechungsbefugnisgrenzen des EuGH. So wurde bereits 1993 in der „Maastricht-Entscheidung“ festgestellt, dass der EuGH „(…) zwischen einer Rechtsfortbildung innerhalb der Verträge (…) und einer deren Grenzen sprengenden, vom geltenden Vertragsrecht nicht gedeckten Rechtssetzung (…)“ zu unterscheiden hat.1 Sollte insoweit methodisch nicht korrekt unterschieden werden, wäre der Rechtsprechung des EuGH nicht zu folgen. Diese Rechtsprechung wurde dann 2009 fortgeführt in der sog. „Lissabon-Entscheidung“.2 Im Jahr 2020 äußerte sich das BVerfG erneut zur juristischen Methodenlehre und führte wörtlich im zweiten Leitsatz des Urteils des zweiten Senates des BVerfG vom 5.5.2020, 2 BvR 859/15 aus: „Der (...) Rechtsprechungsauftrag des Gerichtshofs der Europäischen Union endet dort, wo eine Auslegung der Verträge nicht mehr nachvollziehbar und daher objektiv willkürlich ist. (...)“.
Grundsätzlich verfährt der EuGH anerkanntermaßen nach autonomen europarechtlichen juristischen Methoden, während das BVerfG nach den in Deutschland anerkannten juristischen Methoden verfährt. Des Weiteren wird grundsätzlich der Auslegungs- und Anwendungsvorrang des Europarechts und der Vorrang der Entscheidungsbefugnis des EuGH vor nationalem Recht anerkannt.3 Die zitierten Entscheidungen machen nun aber deutlich, dass die sich ergebenden Systeme wenigstens teilweise deckungsgleich sein müssen, damit festgestellt werden kann, ob vom EuGH angewandte Methoden in der Schnittmenge der Systeme gegeben sind, oder nicht. Im ersten Fall muss nach Auffassung des BVerfG Deutschland nämlich der Rechtsprechung des EuGH folgen, im zweiten Fall nicht, da dann eine demokratische Legitimation fehlt.4 Um diese komplexen Fragen in Zukunft transparent und nachprüfbar und ggf. sogar mittels maschineller Verfahren entscheiden zu können, halten wir eine juristische Methodenlehre 3.0 für erforderlich.5
2.
Der Weg zur Methodenlehre 3.0 ^
Hergebrachte Vorstellungen zur juristischen Methodenlehre seit der historischen Rechtsschule von Friedrich Carl von Savigny (1779–1861) werden hier als Methodenlehre 1.0 bezeichnet. Konzepte zur juristischen Methodenlehre, die darüber hinaus die Erkenntnisse aus dem sog. „linguistic turn“ der Sprachphilosophie berücksichtigen, werden als Methodenlehre 2.0 definiert. Schließlich soll die hier propagierte juristische Methodenlehre, die sich auch darüber hinaus mit (formalen) Systemen der Logik beschäftigt Methodenlehre 3.0 genannt werden.
2.1.
Methodenlehre 1.0 ^
Auch wenn im Einzelnen viele Fragen streitig sind, dürfte im Sinne der so definierten Methodenlehre 1.0 in der Rechtswissenschaft darüber Einigkeit bestehen, dass eine der Hauptaufgaben des juristischen Denkens darin liegt, dass insbesondere Rechtstexte, also Gesetze oder auch Verträge, in einer bestimmten Art und Weise auszulegen bzw. zu interpretieren sind, um deren Bedeutung juristisch korrekt zu ermitteln.6 Im Ergebnis soll durch die juristische Methodenlehre sichergestellt werden, dass die Bedeutung des juristischen Textes, die durch den Urheber (Gesetzgeber oder Vertragspartner) vorgegeben wurde, für die juristische Behandlung des Textes maßgeblich ist und nicht die private Meinung des jeweiligen Juristen, der über den Text zu befinden hat.7 Den Diskussionsstand der überwiegenden Lehre zur heutigen juristischen Methodenlehre 1.0 bis zum sog. „linguistic turn“, kann man exemplarisch bei Zippelius in dessen Buch „Juristische Methodenlehre“ nachlesen. Die Frage der korrekten Verknüpfung der Bedeutung mit den Worten der Rechtsregeln ist nach Zippelius eine Frage der Semantik. Unsere natürliche Sprache, mit der wir unser juristisches Denken in Worten ausdrücken, verfügt aber im Gegensatz zu formalen Sprachen der modernen Logik und Mathematik nicht über eine exakte (definierte) Semantik. Dies führt Zippelius darauf zurück, dass Rechtsnormen weitgehend Erfahrungsinhalte bezeichnen. Diese Wörter, die Erfahrungstatsachen bezeichnen, werden exemplarisch eingeführt – durch praktisches Einüben – und können daher keinen exakten Bedeutungsumfang haben, sondern nur einen „Bedeutungsspielraum“. Wörter sind also grundsätzlich mehrdeutig und haben nicht für alle Menschen die „genau gleiche Bedeutung“ und nach Zippelius oft auch für den einzelnen selbst „nicht einen ganz exakten Sinn“.8 Damit soll die juristische Methodenlehre z.B. auch die Verfahren bereitstellen, um aus der Menge der möglichen Wortbedeutungen des Gesetzestextes, die auf den konkreten Fall zutreffende Wortbedeutung durch Auslegung nach dem Wortlaut, der Teleologie, dem System und der Historie, durch Interessen abwägung und durch Vergleich des zu prüfenden Falles mit ansonsten etwa schon bekannten Präzedenzfällen der Rechtsprechung zu ermitteln.
2.2.
Methodenlehre 2.0 ^
Werden nun aber die zwei folgenden Probleme mit in die methodischen Überlegungen einbezogen, erfolgt der Entwicklungsschritt von der juristischen Methodenlehre 1.0 zu 2.0.
Nach dem sog. „linguistic turn“ ist nämlich erstens zu bezweifeln, dass man überhaupt verlässlich feststellen kann, welche Bedeutung ein bestimmtes Wort bzw. ein bestimmtes Zeichen der „natürlichen Sprache“ hat.9 Es kann daher nicht mehr darauf ankommen zu versuchen, eine etwa feststehende Beziehung zwischen Wort und Bezeichnetem, die irgendwie außerhalb der Vorstellung der interpretierenden Person existiert, zu finden. Es kann nur noch auf die Untersuchung des jeweiligen Gebrauchs des Wortes bzw. Zeichens ankommen, weil nur daraus auf die Bedeutung geschlossen werden kann. Alles ist nur „Sprachspiel“, wobei die Regeln dieses Spieles nicht endgültig festlegbar sind.10 So kommt man heute nicht mehr am berühmten Wort Ludwig Wittgensteins (1889–1951) vorbei: „Die Bedeutung eines Wortes ist sein Gebrauch in der Sprache.“11
Die Worte „Subsumtion“, „Auslegung“ und „Rechtsfortbildung“, die z.B. in den Normen der Rechtsprechungskompetenzen des EuGH im Europarecht vorkommen, sind zweitens ihrerseits, wie alle Worte auslegungsbedürftig, weil es verschiedene methodische Konzepte zu diesen juristischen Verfahrensweisen gibt, denn auch diese Methoden sind exemplarisch eingeführt worden. Es lassen sich also verschiedene (gleichberechtigte) folgerichtige Konzepte von „Subsumtion“, „Auslegung“ und „Rechtsfortbildung“, etc. modellieren.
Beide Problemkreise zusammengenommen führen nun im Rahmen der Methodenlehre 2.0 zu der Forderung, ein Gericht müsse erst aus der Menge möglicher Methoden die für richtig gehaltene Methode auswählen, in Anlehnung an Wittgenstein, also nicht nur ein „Sprach“- sondern auch ein „Methodenspiel“ spielen.12
Im Ergebnis ist nach der Methodenlehre 2.0 für unsere Fragestellung daher zu vertreten, dass die vom BVerfG angemahnten und vom EuGH zu beachtenden methodischen Grenzen durch den EuGH erst in natürlicher Sprache formuliert werden müssen, wobei der EuGH dabei aus der Menge möglicher Methoden die für richtig gehaltene Methode auswählen muss, um sich so eine bindende Methodenlehre überhaupt erst selbst zu schaffen.
2.3.
Methodenlehre 3.0 ^
Da nun Wörter, mögen diese den Norminhalt, den Sachverhalt, Weltwissen, oder eben auch Konzepte der juristischen Methodenlehre beschreiben, stets nur über ihren Gebrauch Bedeutung erlangen bzw. funktionieren, besteht die Gefahr, dass diese Gebrauchszusammenhänge zu komplex werden, als dass man diese ohne Unterstützung informatischer Verfahren noch belastbar prüfen kann.13 Es erscheint notwendig, den Vorteil maschineller Inferenz zur Sicherstellung einer hohen Genauigkeit und Tiefe der notwendigen logischen Schlussfolgerungen in der juristischen Argumentation zu nutzen.
Um nun in unserer Ausgangsfrage weiter zu kommen und entscheiden zu können, ob ein Fall vorliegt, bei dem, wie grundsätzlich die Rechtsprechung des (EuGH) gegenüber der des (BVerfG) vorrangig ist, oder nicht, sind formale (Meta-) Systeme zu formulieren. Dabei ist erneut eine „dritte“ Auswahlentscheidung erforderlich, um aus der Menge möglicher formaler Systeme, ein adäquates System auszuwählen, und dieses als Grundlage einer für EuGH und BVerfG verbindlichen juristischen Methodenlehre 3.0 nutzen zu können.14
Hier soll aus der Menge möglicher formaler Systeme die Familie der sog. Input/Output-Logiken (I/O-Logiken) zur Klärung einer der wichtigsten Rechtsfragen der genannten Entscheidung des BVerfG aus dem Jahr 2020 ausgewählt werden, um exemplarisch darzustellen, wie durch eine Methodenlehre 3.0 maschinell untersucht werden kann, ob das BVerfG dem EuGH folgen muss oder kann – oder ob das BVerfG zutreffend festgestellt hat, dass es dem EuGH nicht folgen darf oder kann.
3.
Formalisierung des Fallgegenstands in Input/Output-Logik ^
Input/Output (I/O)-Logiken wurden von Makinson und van der Torre als eine Klasse von formalen Systemen für normbasierte deontische Schlussfolgerungen entwickelt.15 Intuitiv formalisieren sie die Frage, welche Verpflichtungen aus einer gegebenen Menge von bedingten Normen und einer bestimmten Situation abgeleitet werden können.
Normen werden als Paare (a, x) von Formeln repräsentiert, die Interpretation ist wie folgt: Wenn a der Fall ist, ist x verpflichtend. Eine Menge N solcher Normen wird dementsprechend als N = {(a, x),...} repräsentiert. Vorliegende Tatsachen werden als eine Menge von Formeln A = {a‘, a‘‘,...} repräsentiert; diese Menge bezeichnet man als Input (Eingabe). Ist nun eine Menge N von Normen und ein Input A gegeben, wird in I/O-Logiken der Output (Ausgabe) durch einen Output-Operator out(N, A) = {x‘, x‘‘,...} berechnet. Der Output ist eine Menge von Formeln, die sich als konkrete Verpflichtung durch N und A ergeben.
Die Berechnung der Outputs ist durch die (hier ausgelassene) Definition der out-Operatoren gegeben. Je nach Wahl des Operators können sich verschiedene Outputs ergeben (hier ist also Spielraum für weitere logische Parameter). Die hier verwendete Output-Operation ist der sog. „reusable Output“ (auch out3 genannt). Diese prüft, welche Tatbestandsmerkmale einer bedingten Norm (linke Seite des Paares) durch den Input A erfüllt sind, und fügt dann die entsprechenden Rechtsfolgen dieser Normen (rechte Seite des Paares) dem Output hinzu. Des Weiteren werden die Rechtsfolgen neuerdings als Input wiederverwendet, um weitere sich (transitiv) ergebende Rechtsfolgen abzuleiten. Für formale Details verweisen wir auf die Arbeiten von Makinson und van der Torre.16
3.1.
Kodierung des Sachverhalts ^
Wir beginnen mit der Beschreibung der Tatsachen (Input A). Siehe Tabelle 1 für deren Erläuterung.
| Repräsentation | Beschreibung |
| abstraktGenerellePrüfungEuGH | Der EuGH führt eine abstrakt-generelle Prüfung durch. |
| konkretIndividuellePrüfungEuGH | Der EuGH prüft konkret-individuell. |
| AuslegungDurchEuGH | Der EuGH legt aus. |
| AnwendungDurchEuGH | Der EuGH wendet an. |
| Repräsentation | Beschreibung |
| PrüfungDerAngemessenheitDurchEuGH | Der EuGH prüft die Angemessenheit. |
| korrekteMethodenAnwendungDurchEuGH | Dem EuGH wird methodisch korrekte Arbeit bescheinigt. |
| ultraViresAktDurchEuGH | Der EuGH begeht einen Ultra-Vires-Akt. |
| VorabentscheidungsverfahrenDurchEuGH | Der EuGH führt ein Vorabentscheidungsverfahren durch. |
| VerhältnismäßigkeitsPrüfungDurchEuGH | Der EuGH prüft die Verhältnismäßigkeit. |
| EZBAnleiheKaufEntscheidung | Der konkrete Fall behandelt die Anleihekäufe der EZB. |
| BVerfGFolgtEuGH | Das BVerfG folgt der Auslegung des EuGH. |
Tabelle 1: Übersicht über die verwendeten Symbole in der I/O-Logik-Repräsentation
Jedes Modell von Auslegung und jedes Modell von Anwendung (Subsumtion) muss aufgrund rechtlicher Vorgaben einen Unterschied zwischen Auslegung und Anwendung (Subsumtion) erkennen lassen. Z.B. darf der EuGH im Rahmen eines Vorabentscheidungsverfahrens gem. Art 267 AEUV (im Unterschied z.B. zu einem Vertragsverletzungsverfahren gem. Art. 260 AUEV) das Europarecht nur auslegen, aber nicht anwenden. Letztendlich muss bei allen Modellen der Vorgang der Auslegung abstrakt-generell und der der Anwendung konkret-individuell bleiben, um diesen Unterschied nicht zu verlieren.17 Dies ist implizites Wissen der Methodenlehre 2.0, welches durch die logische Formel …
(A1) ¬(abstraktGenerellePrüfungEuGH ⇔ konkretIndividuellePrüfungEuGH)
… beschrieben werden. (A1) drückt aus, dass abstrakt-generelle Prüfungen nicht identisch zu konkret-individuellen Prüfungen sind. Des Weiteren stellen Auslegungen abstrakt-generelle Prüfungen und Anwendungen konkret-individuelle Prüfungen dar:
(A2) AuslegungDurchEuGH ⇒ abstraktGenerellePrüfungEuGH
(A3) AnwendungDurchEuGH ⇒ konkretIndividuellePrüfungEuGH
Eine konkret-individuelle Prüfung der Angemessenheit im Rahmen der Verhältnismäßigkeitsprüfung ist keine abstrakt-generelle Auslegung mehr, sondern Anwendung (Subsumtion). Hierbei handelt es sich wieder um implizites Wissen im Bereich der Methodenlehre 2.0:18
(A4) PrüfungDerAngemessenheitDurchEuGH ⇒ ¬abstraktGenerellePrüfungEuGH
Das BVerfG führt in Rdn. 119 aus: „Die Auffassung des Gerichtshofs (...) verkennt Bedeutung und Tragweite des auch bei der Kompetenzverteilung zu beachtenden Grundsatzes der Verhältnismäßigkeit (...) offensichtlich und ist wegen der Ausklammerung der tatsächlichen Wirkungen des PSPP methodisch nicht mehr vertretbar (...) Da es sich selbst als Ultra-vires-Akt darstellt, kommt ihm insoweit keine Bindungswirkung zu (cc).“ Hierbei handelt es sich um explizites Wissen im Bereich der Methodenlehre 1.0. Die wird formalisiert durch:
(A5) ¬korrekteMethodenAnwendungDurchEuGH ⇒ ultraViresAktDurchEuGH
(A6) VorabentscheidungsverfahrenDurchEuGH ∧ EZBAnleiheKaufEntscheidung
Des Weiteren wurde eine Verhältnismäßigkeits- aber keine Angemessenheitsprüfung durchgeführt.
(A7) VerhältnismäßigkeitsPrüfungDurchEuGH ∧¬PrüfungAngemessenheitDurchEuGH
Die Formeln (A1) – (A7) bilden nun den Input A für die I/O-Logik-Anwendung:
A = {A1, A2, A3, A4, A5, A6, A7}
3.2.
Kodierung der relevanten Normen ^
In einem zweiten Schritt werden nun die relevanten Menge an Normen N formalisiert, dabei werden wieder auch die Symbole aus Tabelle 1 zurückgegriffen.
Nach BVerfG Rdn. 119 gilt kurz gesagt: Wenn ein Urteil des EuGH einen Ultra-Vires-Akt darstellt, dann darf das BVerfG dem EuGH nicht folgen. Dem steht nicht entgegen, dass das BVerfG grundsätzlich einen Auslegungs- und Anwendungsvorrang des Europarechts und einen Vorrang der Entscheidungsbefugnis des EuGH vor nationalem Recht anerkennt.20 Hierbei handelt es sich um explizites Wissen im Bereich der Methodenlehre 1.0:
(N1) (ultraViresAktDurchEuGH, ¬BVerfGFolgtEuGH)
(N2) (⊤, BVerfGFolgtEuGH)
Es handelt sich bei der Norm (N1) also um eine Ausnahme zu der allgemeinen Norm (N2).
Wenn der EuGH im Verfahren der Vorabentscheidung angerufen wird, darf er (nur) über die Auslegung des Europarechts entscheiden. Die Anwendung des so ausgelegten Europarechts erfolgt dann durch die nationalen Gerichte. Der EuGH darf also im Vorabentscheidungsverfahren Europarecht nicht anwenden. Hierbei handelt es sich um explizites Wissen im Bereich der Methodenlehre 1.0:
(N3) (VorabentscheidungsverfahrenDurchEuGH, AuslegungDurchEuGH)
(N4) (VorabentscheidungsverfahrenDurchEuGH, ¬AnwendungDurchEuGH)
Nach Rdn. 123 gilt: „Der Ansatz des Gerichtshofs, auch im Rahmen der Verhältnismäßigkeitsprüfung (1) die tatsächlichen Wirkungen des PSPP außer Acht zu lassen und eine wertende Gesamtbetrachtung nicht vorzunehmen (2), verfehlt die Anforderungen an eine nachvollziehbare Überprüfung (...). Damit kann der Grundsatz der Verhältnismäßigkeit die ihm (...) zukommende Korrektivfunktion zum Schutz mitgliedstaatlicher Zuständigkeiten nicht mehr erfüllen. Diese Auslegung lässt das Prinzip der begrenzten Einzelermächtigung (...) im Grunde leerlaufen.“ Dem liegt die Norm zu Grunde: Der EuGH muss methodisch korrekt urteilen und dazu ist es erforderlich, den Verhältnismäßigkeitsgrundsatz korrekt anzuwenden:
(N5) (VorabentscheidungsverfahrenDurchEuGH,VerhältnismäßigkeitsPrüfungDurchEuGH)
Nach BVerfG ist nun die nicht erfolgte Prüfung der Angemessenheit durch den EuGH im konkreten Fall ein methodischer Fehler, siehe Rdn. 119: „Die Auffassung des Gerichtshofs in seinem Urteil vom 11. Dezember 2018, (…) ist wegen der Ausklammerung der tatsächlichen Wirkungen des PSPP methodisch nicht mehr vertretbar.“ Daraus ergeben sich die folgenden Normen:
(N6) (VorabentscheidungsverfahrenDurchEuGH ∧ PrüfungAngemessenheitDurchEuGH,
korrekteMethodenAnwendungDurchEuGH)
(N7) (VorabentscheidungsverfahrenDurchEuGH ∧ ¬PrüfungAngemessenheitDurchEuGH
∧ EZBAnleiheKaufEntscheidung, ¬korrekteMethodenAnwendungDurchEuGH)
Eine vom EuGH korrekt durchgeführte Angemessenheitsprüfung ist also nach BVerfG als korrekte Anwendung der Methoden zu interpretieren (N6). Im konkreten Fall ist insbesondere eine vom EuGH ausgebliebene Angemessenheitsprüfung nach BVerfG als methodisch inkorrekt zu interpretieren (N7).
Im Gegensatz dazu ist der EuGH offensichtlich davon überzeugt, im konkreten Fall methodisch korrekt gearbeitet zu haben:
(N8) (VorabentscheidungsverfahrenDurchEuGH ∧ ¬PrüfungAngemessenheitDurchEuGH
∧ EZBAnleiheKaufEntscheidung, korrekteMethodenAnwendungDurchEuGH)
Da der EuGH in anderen Fällen allerdings Angemessenheitsprüfungen im Rahmen von Vorabentscheidungsverfahren durchgeführt hat, scheint er auch dies für methodisch korrekt zu halten:
(N9) (VorabentscheidungsverfahrenDurchEuGH ∧ PrüfungAngemessenheitDurchEuGH,
korrekteMethodenAnwendungDurchEuGH)
Normen (N6) und (N9) sagen also essentiell das Gleiche aus; wir nehmen sie aus Gründen der Transparenz dennoch explizit auf.
Die Normen (N1) – (N9) bilden nun die Normmenge N für die I/O-Logik-Anwendung:
N={N1, N2, N3, N4, N5, N6, N7, N8, N9}
4.
Analyse des Falles mithilfe der Automatisierung von I/O-Logiken ^
Automatisierte Theorembeweiser sind logikbasierte KI-Systeme zum automatischen formalen Schlussfolgern. Aktuelle Forschung im Bereich des „Legal Reasoning“ versucht u.a. solche Technologien für praxisrelevante Anwendungen in der juristischen Argumentation zu entwickeln.
Theorembeweiser für klassische Logik sind für die juristische Domäne ungeeignet: Widerspricht ein Sachverhalt den Anforderungen einer Normmenge N, können hier keine sinnvollen Schlussfolgerungen mehr gezogen werden (siehe (I) unten). Demgegenüber ist es die Stärke moderner, anfechtbarer deontischer Logiken (wie I/O-Logiken) mit Normkonflikten und Pflichtverletzungen umgehen zu können. Allerdings ist die Automatisierung dieser Logiken in der Regel komplexer. Für I/O-Logiken stellte Steen erstmals eine Prozedur zur Automatisierung der Output-Berechnungen für einfache I/O-Logiken vor.21 Für kompliziertere I/O-Logiken (s.u.) präsentiert Steen das Automatisierungssystem rio.22 Die nachfolgenden Ergebnisse wurden automatisch mit rio erzeugt.
Bei naiver Anwendung der Normen auf die konkrete Situation, beide aus Abschnitt 3, ergeben sich widersprüchliche Verpflichtungen: Zum einen ist es generell verpflichtend, dass das BVerfG dem EuGH im Vorabentscheidungsverfahren folgt (N2), zum anderen kann die Verpflichtung, dass das BVerfG dem EuGH nicht folgen darf, durch (N1) in Verbindung mit der Situationsbeschreibung A abgeleitet werden. Dies wird durch den Output …
(I) out3(N, A) = Cn(F)
belegt; dies bedeutet intuitiv, dass jede logische Konsequenz der Falschheit (durch Cn(F) repräsentiert) – also auch widersprüchliche Konsequenzen – abgeleitet werden kann.23 Dieser Widerspruch ließe sich auch in klassischer Logik herleiten, wenn man die Normpaare naiv als materielle Implikationen auffasst.
Nun ist es nicht unüblich, dass sich Normen widersprechen; es ist eben der rechtswissenschaftliche Prozess, in einem konkreten Fall zwischen konkurrierenden Normen auszuwählen. Auf der formalen Seite der I/O-Logiken kann dies durch (a) den Ausschluss von konkurrierenden Normen oder (b) durch Bevorzugung von spezifischen Normen geschehen.
Der Ansatz (a) wird „constrained I/O logic“ (I/O-Logik mit Restriktionen) genannt. Hier werden formale Einschränkungen (constraints) C als logische Formeln postuliert, mit denen die Ausgabe out(N, A) keinen Widerspruch erzeugen darf.24 Um nun weiterhin widerspruchsrobust sich ergebende Verpflichtungen ableiten zu können, haben Makinson und van der Torre ein Verfahren geschaffen, widersprüchliche Verpflichtungen zu entfernen, indem eine sog. maxfamily von Normen gebildet wird: Sie beinhaltet maximale Teilmengen N‘ ⊆ N von Normen die in der Situation A gerade noch logisch mit den Einschränkungen C vereinbare (also nicht widersprüchliche) Outputs erlauben. So werden einige Normen ignoriert, die bei Hinzunahme einen Widerspruch im Output erzeugen würden. Da es mehrere Möglichkeiten gibt, maximale Teilmengen N‘ zu bilden, beinhaltet die maxfamily(N, A, C) mehrere Mengen; sie ist also eine Familie von Teilmengen von N. Intuitiv kann eine maxfamily mit allen Möglichkeiten identifiziert werden, aus den Normen von N auszuwählen, sodass die ausgelösten Rechtsfolgen sich und C nicht widersprechen – wir sprechen von (konsistenten) Auslegungen.25 Die tatsächliche Ausgabe erhalten wir durch Aggregation aller Outputs aller Auslegungen der maxfamily, und zwar entweder durch (a1) die Vereinigung (∪) aller Outputs, genannt „gutgläubiger“ (credulous) Output, oder durch (a2) den Schnitt (∩) aller Outputs, genannt „skeptischer“ (skeptical) Output:
out∪ ∩(N, A, C) = ∩ / ∪{out(N‘, A) | N‘ ∈ maxfamily(N, A, C)}
Intuitiv ist eine Rechtsfolge im gutgläubigen Output enthalten, falls sie aus mindestens einer konsistenten Auslegung folgt. Entsprechend ist eine Rechtsfolge im skeptischen Output enthalten, falls sie aus allen konsistenten Auslegungen folgt.
Im vorliegenden Fall erhalten wir folgende Ergebnisse: Die maxfamily, formal maxfamily(N, A, C), zeigt, dass es nicht klar ist ob nun das BVerfG folgen muss oder nicht folgen darf:
maxfamily(N,A,C) = {{N1, N2, N3, N4, N5, N6, N8, N9},
{N2, N3, N4, N5, N6, N7, N9}, {N1, N3, N4, N5, N6, N7, N9}}
Intuitiv, beschreibt die erste Auslegung den Standpunkt des EuGH, die zweite und dritte den des BVerfG; im letzteren Fall ist eine Konsequenz der natürlichen Normenkonkurrenz zwischen (N1) und (N2) dass zwei Auslegungen den Standpunkt des BVerfG repräsentieren. Dies ist beim EuGH nicht nötig, da die Normenkonkurrenz zwischen (N1) und (N2) nicht zum Tragen kommt, wenn kein Ultra-Vires-Akt vorliegt. Entsprechend der obigen maxfamily ergibt sich der skeptische Output:
(II) out∩(N, A, C) = Cn(VerhältnismäßigkeitsPrüfungDurchEuGH,
AuslegungDurchEuGH, ¬AnwendungDurchEuGH,
korrekteMethodenAnwendungDurchEuGH ⇒ BVerfGFolgtEuGH)
Alle Einträge dieses Outputs sind nun konkrete Verpflichtungen, die durch die I/O-Logik-Anwendung identifiziert werden. Interessant ist dass neben den wenig strittigen Verpflichtungen (hier: des EuGH eine Verhältnismäßigkeitsprüfung durchzuführen, und seitens des EuGH auszulegen aber nicht anzuwenden) keine Aussage gemacht wird, ob das BVerfG dem EuGH folgen muss oder nicht. Es wird lediglich eine Pflicht des BVerfG ausgegeben, dem EuGH zu folgen, falls er methodisch korrekt gearbeitet habe (ohne anzugeben, ob das wirklich der Fall ist), repräsentiert durch die Formel:
korrekteMethodenAnwendungDurchEuGH ⇒ BVerfGFolgtEuGH
Der gutgläubige Output ist wegen dieser verschiedenen Standpunkte bzw. der Unvereinbarkeit ihrer Rechtsfolgen, inkonsistent:
(III) out∪(N, A, C) = Cn(⊥)
Der Ansatz (b) wird „preference-based I/O logic“ (präferenz-basierte I/O-Logik) genannt. Hier wird berücksichtigt, dass in der juristischen Arbeit, basierend auf Kollisionsregeln sowie vorigen Entscheidungen, Kommentaren und Sachverhalten, Normenkonkurrenzen kontextual aufgelöst werden, in dem einigen Normen eine Präferenz über andere zugesprochen wird. Im Fall der Präferenz-basierten I/O-Logik wird dies mit einer Präferenzrelation ≥ ⊆ N × N umgesetzt, d.h. einer reflexiven und transitiven binären Relation auf Normen. Intuitiv ist eine Norm n mindestens ebenso stark präferiert wie eine Norm m falls n ≥ m gilt, und echt stärker präferiert, geschrieben n ≥ m, falls n ≥ m und nicht m ≥ n gilt. Normen können auch unvergleichbar sein (falls weder n ≥ m noch m ≥ n gilt), oder gleich präferiert (falls n ≥ m und m ≥ n), geschrieben n ≃ m. Die Relation ≥ kann durch technische Maßnahmen (sog. liftings) zu einer Präferenzrelation ≥* auf Normenmengen erweitert werden. Den Output präferenz-basierter I/O-Logik wird preferred output genannt und ist wie folgt definiert (analog mit ∪ für gutgläubigen Output):
outP∩(N, A, C) = ∩ {out(N‘, A) | N‘ ∈ maxfamily(N, A, C), N‘ ist maximal bzgl. ≥*}
Es ist sinnvoll anzunehmen, dass N1 N2 (nach lex specialis derogat legi generali); dies ist Wissen aus Methodenlehre 1.0. Nimmt man weiterhin an, dass die Normen (N6), (N7), (N8) und (N9) gleich präferiert sind, also N6 ≃ N7 ≃ N8 ≃ N9, so ergibt sich:
(IV) outP∩(N, A, C) = Cn(VerhältnismäßigkeitsPrüfungDurchEuGH,
AuslegungDurchEuGH, ¬AnwendungDurchEuGH,
korrekteMethodenAnwendungDurchEuGH ⇔ BVerfGFolgtEuGH)
Dies ist eine Verstärkung von Resultat (III), da hier nun auch folgt, dass das BVerfG dem EUGH nicht folgen darf, falls die methodische Arbeit des EuGH als inkorrekt angesehen wird.
Nimmt man stattdessen an, dass N6 ≃ N7, N8 ≃ N9, jedoch {N6, N7} *{N8, N9}, also dass der Standpunkt des BVerfG dem des EuGH vorzuziehen ist, dann ergibt sich:
(V) outP∩(N ,A, C) = Cn(VerhältnismäßigkeitsPrüfungDurchEuGH,
AuslegungDurchEuGH, ¬AnwendungDurchEuGH,
¬korrekteMethodenAnwendungDurchEuGH, ¬BVerfGFolgtEuGH)
Es ergibt sich also insbesondere, dass das BVerfG dem EuGH nicht folgen darf. Ist es hingegen andersherum, also {N8, N9} *{N6, N7}, so folgt:
(VI) outP∩(N, A, C) = Cn(VerhältnismäßigkeitsPrüfungDurchEuGH,
AuslegungDurchEuGH, ¬AnwendungDurchEuGH,
korrekteMethodenAnwendungDurchEuGH,BVerfGFolgtEuGH)
Hier ist es also verpflichtend für das BVerfG dem EuGH zu folgen, da die methodische Arbeit des EuGH als korrekt angesehen werden muss.
Fazit: Logikpluralismus für normatives Schließen ^
Wir plädieren in dieser Arbeit für eine Methodenlehre 3.0, die die Auswahl und Rechtfertigung geeigneter Methoden des allgemeinen Schließens (hier: Logik) zum Gegenstand hat. Wir zeigen erstens die Möglichkeit einer solchen Methodenlehre auf, indem wir beispielhaft einen Diskurs der Methodenlehre 2.0 in I/O-Logik formalisieren. Im Ergebnis erlaubt unsere Formalisierung uns Auslegungen darzustellen, unter denen (a) eine Inkonsistenz des Systems besteht ((I), (III)), (b) eine bedingte Pflicht des BVerfG besteht, dem EuGH bei korrekter Methodenanwendung zu folgen (II), (c) zusätzlich eine bedingte Pflicht des BVerfG besteht, dem EuGH im Falle inkorrekter Methodenanwendung nicht zu folgen (IV), (d) die Methodenanwendung des EuGH als inkorrekt zu bewerten ist und das BVerfG ihm nicht folgen darf (V), und (e) die Methodenanwendung des EuGH als korrekt anzusehen ist und das BVerfG ihm folgen muss (VI). Ein Methodenlehrediskurs 3.0 müsste die Korrektheit und Adäquatheit unserer Formalisierung prüfen. Zweitens demonstrieren wir die Vorteilhaftigkeit der Methodenlehre 3.0, indem wir die obigen Ausgänge des Diskurses automatisch generieren, ihre Korrektheit garantieren und sie anhand der erzeugten Beweise begründen können. Hierfür wurde die rio-Software von Steen genutzt. Drittens weisen wir auf die Notwendigkeit einer Methodenlehre 3.0 hin: Unsere Formalisierung wäre in klassischer Logik nicht möglich, auch die „One-size-fits-all“-Logik gibt es nicht. Im Gegenteil herrscht in der modernen Logik Logikpluralismus:26 Die hier getroffene Auswahl von I/O-Logiken ist nur eine Möglichkeit. Es existieren diverse Logikformalismen für normative, jede mit Vor- und Nachteilen. Es ist wichtig zu unterstreichen, dass sich im Allgemeinen je nach Wahl des Logik-Systems auch die Ergebnisse unterscheiden werden. Im Rahmen der Methodenlehrediskursen 3.0 muss also die Wahl des Formalismus dokumentiert und begründet bzw. kritisiert werden.
Anhang A: Computer-Repräsentation der Fallanalyse ^
Codierung des Sachverhalts wie in Kapitel 3 beschrieben; hier in TPTP-Format zur Nutzung mit rio.
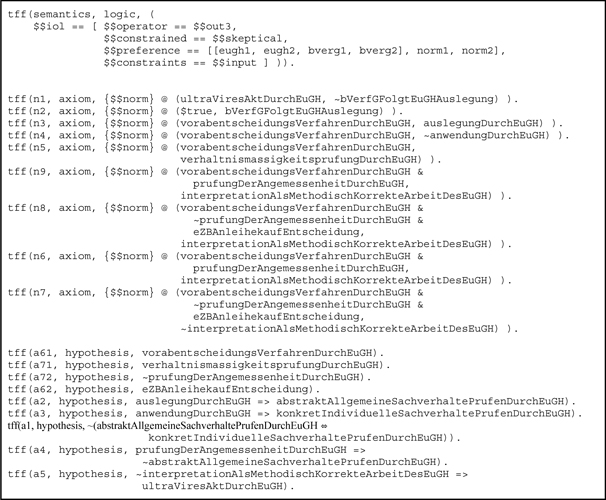
- 1 BVerfG NJW 1993, 3047 ff. (3057).
- 2 BVerfG NJW 2009, 2267 ff.
- 3 Urteil des BVerfG vom 5.5.2020, 2 BvR 859/15 Rdn 112.
- 4 Urteil des BVerfG vom 5.5.2020, 2 BvR 859/15 Rdn 113.
- 5 Es gibt zahlreiche Veröffentlichungen und Forschungsarbeiten über die Repräsentation und Formalisierung von juristischer Argumentation und juristischer Schlussfolgerung. In dieser Arbeit befassen wir uns mit der Fragestellung, ob und wie solche Arbeiten systematisch in eine deutsche juristische Methodenlehre – die Methodenlehre 3.0 – einfließen sollten. Aus Platzgründen kann die Plausibilisierung nur anhand eines beispielhaften Formalismus (hier: Input/Output-Logik) gezeigt werden. Dies ist keine Aussage darüber, dass dieser Formalismus der einzige oder gar der Beste aller existierenden Formalismen ist, sondern dient lediglich der Veranschaulichung. Eine Diskussion, welcher Formalismus tatsächlich für eine von uns vorgestellte Methodenlehre 3.0 adäquat ist, wird in dieser Arbeit nicht geführt; wir laden jedoch alle herzlich ein konstruktiv bei dieser Diskussion mitzuwirken.
- 6 Vgl. z.B. Bydlinski, Juristische Methodenlehre und Rechtsbegriff, Wien/New York 1991, S. 428 ff.; Röhl/Röhl, Allgemeine Rechtslehre, München 2008, S. 24 ff.; Zippelius, Juristische Methodenlehre, München 2021, S. 15 ff. und S. 37 ff.
- 7 Adrian, Grundzüge einer allgemeinen Wissenschaftstheorie auch für Juristen, Berlin 2014, S. 35 f. m.w.N.
- 8 Zum Ganzen siehe nur Zippelius, Juristische Methodenlehre, 2021, S. 89f., 38 m.w.N.
- 9 Siehe hierzu Adrian, Umgang mit natürlicher und formaler Sprache im Recht – von Aristoteles zum Richterautomaten? in Der Wirtschaftsführer 2022, Seite 9 ff. m.w.N.
- 10 Siehe auch Adrian, Grundzüge einer allg.Wissenschaftstheorie auch für Juristen, 2014, S. 65 ff. m.w.N.
- 11 Wittgenstein, Philosophische Untersuchungen, § 43, in: Tractatus Logico-Philosophicus ; Tagebücher 1914–1916; Philosophische Untersuchungen. Werkausgabe von Suhrkamp Taschenbuch, Bd.1, 1. Aufl., Frankfurt a.M. 1984.
- 12 Die Forderung nach einem “Methodenspiel” wurde (soweit ersichtlich bisher ausschließlich) entwickelt in Adrian, Grundprobleme einer juristischen (gemeinschaftsrechtlichen) Methodenlehre, Berlin 2009, S. 745 ff. (775), 945 ff., Adrian, Grundzüge einer allg. Wissenschaftstheorie auch für Juristen, 2014, S. 31 ff., 114 f.
- 13 Zum erforderlichen Ausstieg in eine höhere Komplexität in der juristischen Methodenlehre siehe bereits Adrian, Grundzüge einer allgemeinen Wissenschaftstheorie auch für Juristen, 2014, S 90 f. m.w.N.
- 14 Siehe hierzu bereits erste Hinweise bei Adrian, Rapp, Steen, Von Objekt- und Meta-Ebenen: Analyse der Softwareanforderungen computergestützter juristischer Entscheidungen, in Recht DIGITAL – 25 Jahre IRIS, Tagungsband des 25. Internationalen Rechtsinformatik Symposiums IRIS 2022, Bern 2022, Seite 307 ff.
- 15 Siehe Makinson und van der Torre, Input/Output Logics. J. Philos. Log. 29(4): 383-408 (2000).
- 16 Makinson und van der Torre, Input/Output Logics. J. Philos. Log. 29(4): 383-408 (2000).
- 17 Adrian, Grundprobleme einer juristischen (gemeinschaftsrechtlichen) Methodenlehre, Berlin 2009, S. 777 ff., insbesondere S. 813 ff.
- 18 Adrian, Juristische Methodenlehre und die „Keck-Entscheidung“ des EuGH, in: Europäisches Wirtschafts- und Steuerrecht 1998, S. 288 ff.; Adrian, Grundprobleme einer juristischen (gemeinschaftsrechtlichen) Methodenlehre, Berlin 2009, S. 813 ff.
- 19 https://curia.europa.eu/juris/liste.jsf?language=de&num=C-493/17.
- 20 Urteil des BVerfG vom 5.5.2020, 2 BvR 859/15 Rdn 112.
- 21 Siehe Steen, Goal-Directed Decision Procedures for Input/Output Logics, DEON, College Publications, 2021.
- 22 Siehe Steen, aureleeNet/rio: rio 1.2, Zenodo, 2022. URL: https://doi.org/10.5281/zenodo.7081331.
- 23 In klassischer Logik folgt aus falschem Beliebiges (Ex falso quodlibet), genannt “Prinzip der Explosion“.
- 24 Dies bedeutet insbesondere, dass der Output out(N,A) nicht zu sich selbst widersprüchlich sein darf.
- 25 Im Rahmen dieser Arbeit wird C = A gesetzt. Siehe Makinson, van der Torre, 2000.
- 26 A.A.: Stei, E. „Disagreement about logic from a pluralist perspective“. Philos Stud 177, 3329–3350 (2020).





