Jusletter IT

In der rechtswissenschaftlichen Literatur wird bereits seit langer Zeit vertreten, dass juristischen Entscheidungen (auch) logische Schlussfolgerungen zugrunde liegen¹ und zum Teil auf einen sog. Justizsyllogismus verwiesen.² Was läge also näher, als logikbasierte KI-Systeme einzusetzen, um – entsprechend dieser Auffassung von juristischer Methodenlehre – maschinelle Verfahren zur Unterstützung von Gerichten und Behörden zu implementieren. Und tatsächlich werden seit Jahren in der Steuerverwaltung erfolgreich u.a. mittels eines sog. “Expertensystems”, also mittels symbolischer KI-Verfahren, Steuersachverhalte vollautomatisch geprüft und Steuerbescheide in sehr großer Zahl vollautomatisch erstellt.³ Im IRIS Tagungsband 2022 haben wir bereits die Möglichkeit symbolischer KI-Verfahren zur computergestützten Entscheidungsfindung⁴ vorgestellt und in dem von 2023 eine Maschine erläutert, welche die Konsistenz juristischer Argumentationen in einer Bundesverfassungsgerichtsentscheidung mittels Theorembeweisern prüfen kann.⁵ Auch zur Unterstützung der Gesetzgebung in Österreich werden maschinelle Schlussverfahren unter dem Stichwort “law as code” im Rahmen eines Proof of Concept eingesetzt, um z.B. die Widerspruchsfreiheit von Rechtsnormen zu gewährleisten.⁶ Schließlich starten wir nächstes Jahr ein größeres Forschungsprojekt, bei dem es auch um die maschinelle Unterstützung von Notariaten und Registergerichten in Deutschland gehen soll, indem z.B. evaluiert wird, inwieweit Anmeldungen von neu gegründeten GmbHs und deren Vollzug im Handelsregister über maschinelle Subsumtionsschlüsse für die menschlichen Sachbearbeiter vorgeprüft werden können. Aus juristischer Sicht würden wir wohl cum grano salis bei all diesen “Maschinen” pauschal von Subsumtionsautomaten sprechen, wohingegen es im vorliegenden Beitrag aus Informatiksicht zunächst nur um symbolische Deduktionsverfahren der Künstlichen Intelligenz gehen soll, wenn auch diese Deduktionsmaschinen, nennen wir sie M, typischerweise nur in Kombination mit weiteren Verfahren eingesetzt werden, um als Teilkomponente innerhalb eines juristischen KI-Gesamt-Systems J, entsprechend eines spezifischen juristischen Einsatzzweckes (Verwaltungsakterzeugung, Entscheidungsfindung, Urteilsüberprüfung, überwachter Normerlass, Registerassistent) zu funktionieren.

Zukünftig wird sich ein umfassender Rechtswandel beim Einsatz von KI vollziehen. Auf der europäischen Ebene befindet sich der Entwurf der „Verordnung des Europäischen Parlaments und des Rates zur Festlegung harmonisierter Vorschriften für Künstliche Intelligenz (Gesetz über Künstliche Intelligenz) und zur Änderung bestimmter Rechtsakte der Union“ vom 21.4.2021, samt überarbeitetem Ratsvorschlag vom 6.12.2022, (KI-VO-E) in Entwicklung.⁷ Unter einem KI-System versteht Art. 3 I Nr. 1, Anhang I KI-VO-E nicht nur Konzepte des maschinellen Lernens, sondern auch Logik- und wissensgestützte Konzepte, einschließlich Wissensrepräsentation, induktiver (logischer) Programmierung, Wissensgrundlagen, Inferenz- und Deduktionsmaschinen, (symbolischer) Schlussfolgerungs- und Expertensysteme. Werden KI-Systeme in besonders grundrechts-sensiblen Bereichen eingesetzt, so können sie nach Art. 6 KI-VO-E als Hochrisiko-KI-Systeme gelten und unterliegen nach Art. 8 KI-VO-E zahlreichen Anforderungen. Danach ist die Einhaltung der Zweckbestimmung (Art. 3 Nr. 12 KI-VO-E) des Hochrisiko-KI-Systems und die Einrichtung eines Risikomanagementsystems (Art. 9 KI-VO-E) zu gewährleisten. Damit das Risikomanagementsystem als kontinuierlicher iterativer Prozess erfolgreich sein kann, müssen gem. Art. 9 V-VII KI-VO-E geeignete Testverfahren für das jeweilige Hochrisiko-KI-System eingesetzt werden. Ein Ziel ist es, anhand zuvor festgelegter Parameter und probabilistischer Schwellenwerte (Art. 9 VII 2 KI-VO-E) die Erfüllung der Zweckbestimmung zu testen. So müssen nach Art. 15 I, II KI-VO-E Hochrisiko-KI-Systeme im Hinblick auf ihre Zweckbestimmung ein angemessenes Maß an Genauigkeit, Robustheit und Cybersicherheit erreichen und die Genauigkeitsgrade sowie die relevanten Genauigkeitskennzahlen in der Gebrauchsanweisung enthalten sein.

Die im KI-VO-E notwendigerweise allgemein genannten Anforderungen müssen anwendungsspezifisch – hier zur Anwendung gerade auf symbolische KI-Verfahren – ausgelegt werden. Dabei fokussieren wir uns auf vier zentrale Aspekte der Evaluation, die sich aus unseren Ausführungen ergeben: Erfüllung der Zweckbestimmung (4.1.), Genauigkeit (4.2.), Risikoabschätzung (4.3.) und Robustheit (4.4.).

Neben den aktuell populären KI-Methoden des maschinellen Lernens zählen auch symbolische Verfahren zu den verbreiteten Ansätzen im Feld der Künstlichen Intelligenz. Symbolische KI-Verfahren repräsentieren Domänenwissen, -regeln oder -prinzipien (allgemein: Daten) durch geeignete symbolische und maschinen-verarbeitbare Darstellungen, und verarbeiten diese durch gezielte Manipulation der Dateneinheiten. Dabei kann die symbolische Repräsentation viele Formen annehmen, und z.B. in kontrollierter natürlicher Sprache, als logik-basierter mathematischer Formalismus, oder als programmiersprachenähnliches Konstrukt vorliegen. Jeder Repräsentationsform ist hierbei gemein, dass die verarbeiteten Daten als semantikbehaftete (wenngleich oftmals technische) Artefakte vorliegen, und damit eine explizite Bedeutung bzw. Funktion innehaben. Die jeweiligen symbolischen KI-Verfahren legen dann fest, nach welchen Prinzipien diese Daten modifiziert, ergänzt oder anderweitig verarbeitet werden. Dies steht im Kontrast zu den subsymbolischen KI-Verfahren⁸, z.B. Methoden des maschinellen Schließens, bei denen die gesammelten Informationen statistisch repräsentiert werden. In diesem Kontext liegt das eigentliche Wissen “dezentral”, als emergente Semantik des gesamten komplexen statistischen Systems, vor. Eine inhärente Eigenschaft von symbolischen KI-Systemen ist ihre Erklärbarkeit und Transparenz: Gerade weil die Daten symbolisch repräsentiert und verarbeitet werden, können Verhalten oftmals einfacher gesteuert, nachvollzogen und angepasst werden (z.B. bei unerwünschtem Verhalten bzw. Fehlfunktionen). Bei subsymbolischen Verfahren ist dies in der Regel schwierig, da das Verhalten des Systems nicht explizit beschrieben und damit greifbar ist, sondern sich latent aus der Gesamtheit der statistischen Daten ergibt. Symbolische KI-Verfahren finden sich z.B. in Experten- und Diagnosesystemen, Logik- und Argumentationssystemen, sowie in Konfigurations- bzw. Optimierungskontexten.

Eine spezielle Klasse von symbolischen KI-Systemen sind Systeme zum automatischen bzw. computergestützten logischen Schlussfolgern (engl. automated reasoning). Unter dem Oberbegriff der Logikautomatisierung fallen u.a. sogenannte SAT-Solver, SMT-Solver, Beweisassistenten und Theorembeweiser⁹. Die von dieser Art von Software verarbeiteten symbolischen Daten bestehen in der Regel aus logischen Formeln (in maschinenlesbarem Format) oder logik-ähnlichen mathematisch-formalen Beschreibungssprachen. Schlussfolgerungs-Programme automatisieren einen logischen Ableitungsprozess der aus vorhandenem Wissen mithilfe des Prinzips der Deduktion neues Wissen generiert. Die deduktiven Ableitungsschritte sind dann durch entsprechende logische Schlussprinzipien gerechtfertigt. Solche Softwaresysteme werden Deduktionsmaschinen genannt.

Deduktionsmaschinen decken nur einen kleinen Teil der Bandbreite symbolischer KI-Methoden und -Anwendungen ab. Weitere relevante, aber hier nicht behandelte symbolische KI-Verfahren umfassen z.B. induktive (und abduktive) Logik-Programmierung, Wissensrevision (engl. belief revision), Planung, kombinatorische Optimierung, und symbolische Sprachverarbeitung. Symbolische KI-Verfahren werden bereits in akademischen und industriellen Anwendungen genutzt, z.B. in der mathematischen Grundlagenforschung, für die Verifikation von (kritischen) Software- und Hardwaresystemen, und zum Entwurf und zur Analyse von Regelsystemen.

Für die Evaluation wird eine hypothetische und abstrakte normative Deduktionsmaschine M im Sinne von 3.1 oben betrachtet, welche als Teilkomponente eines juristischen KI-Systems J eingesetzt wird. M wird dabei als eine vollständig automatische Komponente angenommen, bedarf also keinerlei menschliche Interaktion; J ist dagegen nicht notwendigerweise vollautomatisch, sondern ggf. ein dialogisches System, welches teil-automatisiert menschliche Nutzer unterstützt bzw. berät. Der genaue Aufbau und Zweck von J ist nicht weiter relevant, da die Anforderungen des KI-VO-E für das KI-Teilsystem M Gegenstand der Betrachtung sind. Intuitiv könnte J ein System zur computergestützten Auffindung von relevanten Rechtsnormen sein, oder – im Sinne einer Methodenlehre 3.0¹⁰ – ein System zur (logischen) Plausibilitätsprüfung von juristischen Argumentationen.¹¹ Sei M nun also eine normative Deduktionsmaschine, welche auf einem bestimmten (normativen) Logik-Formalismus basiert, als Eingabe formal repräsentierte Informationen über Sachverhalte und Normen erhält, und als Ausgabe alle durch den gegebenen Sachverhalt ausgelösten Rechtsfolgen ableitet.¹²

Die Zweckbestimmung eines KI-Systems wird nach Art. 3 Nr. 12 KI-VO-E durch die Angaben des Anbieters zur Verwendung des KI-Systems bestimmt. Ob das KI-System fähig ist, die Zweckbestimmung zu erfüllen, richtet sich nach der Leistung eines KI-Systems (Art. 3 Nr. 18 KI-VO-E).

Im Kontext von M und anderen Deduktionsverfahren der symbolischen KI kann die Leistung des Systems durch unüberwindbare theoretische Limitationen grundsätzlich eingeschränkt sein:

• Adäquatheit. Ein Logik-Formalismus L wird in der Regel für einen bestimmten Zweck entwickelt; daher weichen die Eigenschaften von L und die mit L auf Grundlage einer Wissensbasis W erreichbaren Schlussfolgerungen möglicherweise stark von anderen Logiken ab. So ist z.B. klassische Prädikatenlogik (erster Stufe) ein verbreitetes Logik-System für mathematische Anwendungen; lineare Logiken kommen insbesondere zur formalen Modellierung von verbrauchbaren Ressourcen zum Einsatz; Modallogiken zur Darstellung von sprachlichen Modalitäten (möglich, notwendig, ...); nichtmonotone Logiken zur Behandlung von unvollständigem Wissen oder Ausnahmen. Basiert nun M auf Logik L, ist die Adäquatheit von L für die Erfüllung der Zweckbestimmung des Systems essentiell, und dabei unabhängig von der ingenieurtechnischen Implementierungsqualität. So ist z.B. hinreichend bekannt, dass klassische Logiken wie Aussagen- oder Prädikatenlogik für die Darstellung von deontischen und normativen Schlussprinzipien ungeeignet sind. Vor der technischen Entwicklungsarbeit des Softwaresystems muss also die grundlegende Adäquatheit des zugrundeliegenden Formalismus, hier L, reflektiert werden. Für M bedeutet dies, dass L ein Formalismus sein muss, der normative Schlussfolgerungen (in dem gegebenen Rahmen) und die üblichen Phänomene juristischer Argumentation (nicht-monotonie, Normenkonflikte, Normlücken, Normenpräferenzen u.a.) adäquat abbilden kann. Ebenso muss sichergestellt werden, dass das in W enthaltene Wissen das abzubildende Rechtsgebiet adäquat repräsentiert. Bei der 2023 auf der IRIS präsentierten “Urteilsüberprüfungsmaschine” kommt es daher z.B. entscheidend darauf an, dass die implementierte Logik für das jeweilige Rechtsgebiet auch adäquate, also überzeugende Ergebnisse liefert. Argumentative Widersprüche in einer Gerichtsentscheidung können nicht mit jeder Logik aufgedeckt werden.
• Entscheidbarkeit. Eine intrinsische formale Eigenschaft einer Logik L ist ihre Entscheidbarkeit¹³, die entweder vorliegt oder nicht. Informell beschreibt die Entscheidbarkeit die grundsätzliche Umsetzbarkeit eines Softwaresystems, welches garantiert für jede Eingabe (in endlicher Zeit) zu einem (garantiert korrekten) Ergebnis kommt; z.B. der Gültigkeit einer Schlussfolgerung bzw. die Ungültigkeit dieser. Unentscheidbarkeit liegt vor, wenn abstrakt mathematisch gezeigt werden kann, dass ein solches Verfahren nicht existieren kann. So ist die Frage, ob eine Schlussfolgerung in klassischer Prädikatenlogik erster Stufe gültig ist, unentscheidbar. Für M bildet die (Un-)Entscheidbarkeit der zugrundeliegenden Logik eine unumgehbare technische Limitation, die die Erfüllung der Zweckbestimmung hemmen kann. So führt eine unentscheidbare Logik L dazu, dass M höchstens eine „best effort“-Automatisierung darstellt und ggf. nicht erschöpfend alle Rechtsfolgen generieren kann. Dies kann z.B. bedeuten, dass ein konkretes Zeitlimit für die Ausführung von M genutzt werden muss, wobei nach Erreichen des Zeitlimits M extern gestoppt wird – auch wenn ggf. noch nicht die gewünschten Ergebnisse produziert worden sind. Für die “Urteilsüberprüfungsmaschine” bedeutet dies, dass z.B. tiefliegende argumentative Fehler nicht erkannt werden bzw. nicht alle Konsequenzen aus einem gegebenen Urteil abgeleitet werden können.
• Effizienz/Effektivität. Entscheidbare Logik-Formalismen garantieren lediglich, dass eine Ausgabe prinzipiell (in endlicher Zeit) berechnet werden kann. Für die Erfüllung der Zweckbestimmung von M kann es aber auch relevant sein, wie schnell Ergebnisse berechnet werden können. Die sog. Effizienz (oder Komplexität) des Verfahrens beschreibt abstrakt die anzunehmende Berechnungsintensität. Schon bei vergleichsweise simplen Logiken wie der klassischen Aussagenlogik sind die Berechnungsverfahren bereits ineffizient, sodass im schlimmsten Fall viele (lange) Berechnungen nötig sind, um zu einem Ergebnis zu kommen. Mit steigender Rechenleistung von Computersystemen wird dieses Maß ggf. abgedämpft, jedoch nicht eliminiert. In der praktischen Anwendung von Logik-Systemen wird auch die Effektivität eines Systems betrachtet, welche versucht anzugeben, wie gut das System „in der Regel“ funktioniert, auch wenn es insgesamt (d.h im ungünstigsten Falle) eine hohe Komplexität aufweist.¹⁴ Für M kann dies relevant sein, wenn Ergebnisse im Kontext eines dialogischen Systems schnell vorliegen müssen, und die Berechnungen nicht mehrere Minuten oder sogar Stunden in Anspruch nehmen dürfen. Der “digitale Registerassistent” muss z.B. im Echtbetrieb in Notariaten und Registergerichten funktionieren. Eine Zeitersparnis für die Mitarbeitenden ergibt sich nur, wenn die juristischen Vorprüfungen in der Maschine den Arbeitsablauf nicht verzögern.

Zusätzlich zur Leistung des Systems ist auch seine Beherrschbarkeit durch den Nutzer entscheidend, um die Zweckerfüllung zu garantieren:

• Erklärbarkeit. Die Erklärung einer juristischen Schlussfolgerung ist häufig wichtiger als die Schlussfolgerung selbst. Sie ist zudem grundlegend für die Beherrschbarkeit, da das Verständnis des Systems zielgerichtete Eingriffe ermöglicht. M verwendet zur Ableitung von Schlussfolgerungen ein formales Regelwerk K (genannt Kalkül). Bei K könnte es sich z.B. um einen Kalkül des natürlichen Schließens oder einen sogenannten Resolutionskalkül handeln. Die Abfolge der Regelanwendungen nach K (d.h. der Beweis), die M zur Ableitung einer Rechtsfolge vorgenommen hat, kann gleichzeitig als eine Erklärung dienen. Die Nützlichkeit dieser Erklärung hängt maßgeblich davon ab, wie eng K die menschlichen Denkgewohnheiten widerspiegelt. Darüber hinaus werden Techniken zur Nachbearbeitung des Beweises verwendet, z.B. durch Auslassen oder Kollabieren “uninteressanter” Bestandteile wie etwa sich wiederholender Teilbeweise, die Übersetzung des Beweises in natürliche Sprache oder gar ein komplettes Umschreiben des Beweises in einen nutzerfreundlicheren Kalkül K’. Wenn der “digitale Registerassistent” die Eintragung der Handelsregisteranmeldung empfiehlt, oder aber deren Ablehnung, kommt es ersichtlich darauf an, die juristische Begründung hierfür zu kennen. Hierzu ist jedenfalls auch die Erklärbarkeit der Schlussfolgerungen der verwendeten Deduktionsmaschine eine zentrale Voraussetzung.
• Anpassbarkeit. Die offensichtlichste Form der Anpassbarkeit eines Systems ist die Möglichkeit der direkten Zielvorgabe. Bei M geschieht dies durch Stellen einer Anfrage A, z.B. über die Ableitbarkeit einer gegebenen Rechtsfolge. Darüber hinaus kann es für den Nutzer auch möglich sein, in die Wissensbasis W einzugreifen. Seltener umgesetzt sind Systeme die auch einen Wechsel des Kalküls K ermöglichen. Entscheidend für die Anpassbarkeit durch den Nutzer ist das Vorhandensein und die Ausgestaltung von Nutzerinterfaces für A,W, und K, die möglichst wenig technisches Vorwissen erfordern. Beispiele hier umfassen kontrollierte natürliche Sprache, Mark-up bzw. Annotationswerkzeuge für juristische Texte, oder direkte Beigabe maschinenlesbarer Versionen zu juristischen Texten (“Rules-as-Code”). Mit der “Urteilsüberprüfungsmaschine” konnte z.B. gezeigt werden, wie sich der Wechsel des in der Deduktionsmaschine verwendeten Kalküls K auf das Ergebnis der Urteilsüberprüfung auswirkt.

Insbesondere ihre prinzipielle Erklärbarkeit wird oft als Vorteil (deduktiver) symbolischer Verfahren genannt. Allerdings ist die Umsetzung von Beherrschbarkeitsaspekten in der Praxis herausfordernd und weiterhin Gegenstand aktueller Forschung.

Für die Genauigkeit eines KI-Systems verlangt Art. 15 II KI-VO-E die Angabe von Genauigkeitskennzahlen, wobei die dazu herangezogenen Kennzahlen dem Stand der Technik entsprechen (Art. 9 III KI-VO-E) müssen.

Im Kontext von Deduktionsmaschinen kann Genauigkeit sowohl auf der Basis von theoretischen Resultaten als auch durch Zuhilfenahme von empirischen Messungen ausgelegt werden.

• Korrektheit. Die Korrektheit einer Deduktionsmaschine ist eine formale Eigenschaft, die zusichert, dass alle abgeleiteten logischen Schlüsse tatsächlich auch gültige Konsequenzen bzw. gültige Ausgaben sind. Es wäre ein erheblicher Mangel in der Genauigkeit des Systems, wenn es sich bei Ausgaben um Falschinformationen handelt. Korrektheit könnte auch als Eigenschaft für die Erfüllung der Zweckbestimmung interpretiert werden. Der “digitale Registerassistent” gibt z.B. aufgrund eines logischen Fehlschlusses aus, dass der Vollzug davon abhängt, dass ein Gesellschafterbeschluss oder eine Vollmachtsbestätigung nachgereicht wird, obwohl rechtsdogmatisch sowohl ein Gesellschafterbeschluss, als auch eine Vollmachtsbestätigung erforderlich ist.
• Vollständigkeit. Die Vollständigkeit einer Deduktionsmaschine ist ebenfalls eine formale Eigenschaft des zugrundeliegenden Logik-Formalismus. Diese sichert zu, dass alle Ableitungen auch tatsächlich vom System ausgegeben werden. Man beachte, dass es sich dabei um eine von der Korrektheit unabhängige Eigenschaft handelt: Korrektheit beschreibt, dass keine Falschausgaben passieren; Vollständigkeit jedoch, dass alle Soll-Ausgaben auch ausgegeben werden. Wenn der Logik-Formalismus zu “schwach” ist, kann der “digitale Registerassistent” zwar z.B. ableiten, dass ein Gesellschafterbeschluss nachzureichen ist, aber nicht, dass auch zusätzlich noch eine Vollmachtsbestätigung fehlt.
• Redundanz. Soll die Deduktionsmaschine M alle abgeleiteten Rechtsfolgen ausgeben, so kann es ein Aspekt der Genauigkeit von M sein, dass jede Ausgabe nur einmal erzeugt wird; insbesondere sollen Ausgaben nicht bereits aus anderen ableitbar sein, da diese Ausgaben dann redundant wären und unnötige Daten repräsentieren. Der “digitale Registerassistent” soll z.B. nicht sowohl für denselben Fall die Nachreichung eines Gesellschafterbeschlusses verlangen als auch die Nachreichung eines Gesellschafterbeschlusses und die Nachreichung einer Vollmachtsbestätigung.
• Empirische Qualität. Die tatsächliche Softwarequalität kann zumindest in Teilen durch systematische Tests sichergestellt werden; darunter fallen z.B. die Abwesenheit von Implementierungsfehlern, die Qualität von Systemrückmeldungen, die Verständlichkeit der Interaktionsmöglichkeit des Users, und viele mehr. Hier können alle oben genannten Fehler vorkommen – die Ursache liegt nicht in W oder L, sondern in der Implementierung von M.

Das Tatbestandsmerkmal Genauigkeitskennzahlen dürfte derzeit zur Beurteilung symbolischer KI-Verfahren noch offen sein, weil nur schwer argumentierbar ist, was darunter im Kontext von Deduktionsmaschinen verstanden werden soll. Die Anforderungen der Korrektheit und Vollständigkeit sind bivalente Eigenschaften – sie liegen vor oder nicht. Ebenso werden durch empirische Messungen der Systeme unter Laborbedingungen keine verallgemeinerbaren Resultate erzeugt, die als Qualitätsschwellen bzw. allgemeine Kennzahlen dienen können. Je nach Anwendungsbereich können sehr verschiedene empirische Erfolgsquoten den aktuellen Stand der Technik reflektieren.

Als Alternative zu Genauigkeitskennzahlen könnte der Grad der formalen mathematischen Verifizierbarkeit des Softwaresystems dienen (statt oder zusätzlich zu Softwaretests).

Das Risikomanagement nach Art. 9 KI-VO-E verpflichtet zur Ermittlung und Analyse der bekannten und vorhersehbaren Risiken, einer Abschätzung und Bewertung der Risiken sowie schlussendlich die Ergreifung geeigneter Risikomanagementmaßnahmen, damit das Hochrisiko-KI-System im Rahmen der Zweckbestimmung oder einer vernünftigerweise vorhersehbaren Fehlanwendung verwendet werden kann. Die Risikomanagementmaßnahmen tragen gem. Art. 9 III 2 KI-VO-E dem allgemein anerkannten Stand der Technik Rechnung.

Im Kontext der Deduktionsmaschine M können Risiken sowohl durch Implementierfehler als auch durch ungeeignete Benutzung entstehen:

• Auch wenn die theoretischen Eigenschaften des zugrundeliegenden Logik-Formalismus für die Anwendung adäquat sind (siehe Abschnitt 4.1), können softwaretechnische Mängel der Implementierung zu fehlerhaften Ausgaben führen. Dadurch ist direkt auch die Genauigkeit des Systems (siehe Abschnitt 4.2) betroffen.
• Weiterhin kann eine unsachgemäße Benutzung von M zu Risiken führen; dies tritt z.B. ein, wenn die Ausgaben des Systems falsch interpretiert oder unreflektiert in einem anderen Kontext verwendet werden. Eine weitere typische Fehlanwendung ist die unabsichtliche “Trivialisierung” der Wissensbasis W. Diese kann entweder durch eine Inkonsistenz der in W enthaltenen Informationen entstehen, welche es in klassischen Logiken erlaubt beliebiges zu schlussfolgern; oder sie kann durch das unbewusste Hinzufügen von “Kurzschlüssen” hervorgerufen werden, welche die “zu einfache” Ableitung eigtl. komplexer Rechtsfolgen ermöglichen. Hier ist darauf hinzuweisen, dass Rechtsnormen in natürlicher Sprache erlassen werden und damit naturgemäß stets auslegungsbedürftige und mehrdeutige, also auslegungsfähige Normtexte vorliegen, die erst über den Prozess der Formalisierung zu einer maschinenverarbeitbaren Wissensbasis W “umgeschrieben” werden müssen. Hierbei können verschiedenste Fehler passieren, die bei der “Urteilsüberprüfungsmaschine”, oder beim “digitalen Registerassistenten” zu einer unsachgemäßen Benutzung führen können.
• Die Implementation von M kann selbst zu unsachgemäßer Benutzung führen. Für M muss sichergestellt werden, dass die maschinell abgeleiteten Rechtsfolgen nachvollzogen werden können, und Nutzer nicht verleitet werden, die Ausgaben unreflektiert zu verwenden.

Die Softwarequalität, also die Abwesenheit von softwaretechnischen Mängeln, kann durch geeignete und in der Software-Entwicklung etablierte Verfahren unterstützt werden (z.B. Testverfahren). Ebenso könnte es Teil von Risikomanagementmaßnahmen sein, von M zu verlangen, dass jede Ausgabe transparent und extern verifizierbar “begründet” wird. Solche technischen Artefakte können dann von unabhängigen Systemen auf Korrektheit überprüft werden.

Ein angemessenes Maß an Robustheit eines KI-Systems verlangt Art. 15 I KI-VO-E. Damit ist eine technische Redundanz gemeint, die eine Widerstandsfähigkeit gegenüber Risiken im Zusammenhang mit den Grenzen des Systems sowie die Sicherheit gegenüber böswilligen Eingriffen gewährleistet, wie Art. 15 III und Erwg. 50 S. 2 KI-VO-E ausführen. Ziel ist es, die Sicherheit des KI-Systems durch Gefährdungen und schädlichen oder anderweitig unerwünschten Verhalten zu erhalten.

Natürlich kann es vorkommen, dass einzelne Systemkomponenten, durch (software-)technische Mängel ausfallen, falsche Ergebnisse liefern oder das System bzw. seine Geschichte manipulierbar sind – diese Situation unterscheidet sich kaum von anderen komplexen Softwaresystemen, und wird hier darum nicht vertieft diskutiert. Im Kontext von Logik-basierten symbolischen KI-Systemen, wie der Deduktionsmaschine M, können allerdings weitere Dimensionen von Robustheit angelegt werden:

• Eingabestabilität: Üblicherweise können im Kontext von Deduktionsmaschinen die Eingaben verschiedene Methoden der Formalisierung nutzen und daher auf verschiedene syntaktische Darstellungsformen zurückgreifen – welche aber (für den Anwendungskontext) semantisch äquivalent sind. Daraus folgt, dass ein und dieselbe Information, die M als Eingabe erhält, in vielen verschiedenen Formen dargestellt werden kann (man denke z.B. an andere natürlichsprachliche Formulierungen derselben Information). Ein Aspekt von Robustheit von M ist es dann, dass jede Darstellung derselben Eingabeinformationen zum gleichen Ergebnis führt. Als nicht-funktionale Eigenschaft sollten dabei auch die Ausführungseffizienz bzw. -effektivität nicht beeinflusst werden. Zu beachten sind hier die nicht immer klaren Grenzen des Systems: wenn das System etwa zwei Logiken L und L’ akzeptiert, können unterschiedliche Eigenschaften von L und L’ – wie etwa ihre Nähe zur natürlichen Sprache oder ihre Ausdruckskraft – bereits bei der Formalisierung ein und desselben Sachverhalts durch menschliche Kodierung zu semantisch nicht mehr äquivalenten Ergebnissen führen.
• Eingaberobustheit: Die Eingaben eines konkreten Systems werden üblicherweise in einem fest vereinbarten Format formuliert und übergeben. Dennoch können natürlich (ggf. vorsätzlich) nicht wohlgeformte Eingaben an M übergeben werden. Ein Aspekt der Robustheit ist, wie das System auf nicht wohlgeformte Eingaben reagiert: Idealerweise sollte ein System hier entweder spezifizierte Fehlermeldungen bzw. Rückgaben liefern und die Bearbeitung verweigern oder versuchen, die intendierte Eingabe zu inferieren und ggf. im Dialog mit dem Nutzer zu bestätigen. Das Verhalten in diesen Fällen muss entsprechend dokumentiert sein.
• Plausibilität: Werden Eingabeinformationen von M vor Bearbeitung auf ihre Plausibilität überprüft? Dadurch könnten Bedienfehler zumindest eingeschränkt werden, und so nicht intendierte Ausführungen vermieden werden. Unplausible Eingaben könnten im Kontext von M zum Beispiel leere Normenmengen sein, Normen ohne Rechtsfolge und/oder Tatbestandsmerkmale, und Normen mit eindeutig nicht erfüllbaren Tatbestandsmerkmalen.

Zwar können einige der oben genannten Qualitätskriterien durch mathematische Methoden formal verifiziert werden, allerdings ist dies zeit-intensiv, schwierig und muss nach jeder Erweiterung des Systems wiederholt werden. Daher hat es sich durchgesetzt, die Qualität und Effektivität von Deduktionsmaschinen im Allgemeinen durch empirische Evaluationsverfahren zu erheben.

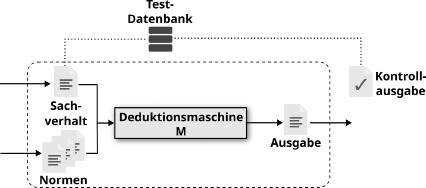
Abbildung 1: Aufbau eines empirischen Testverfahrens für M.

Abbildung 1 zeigt einen beispielhaften Aufbau einer solchen Evaluation. Dabei werden die Deduktionsmaschine M und die zugrundeliegenden Normen fixiert, die Testfälle aber aus einer zuvor gesammelten Datenbank entnommen. Jeder Testfall spezifiziert die Eingaben (hier: Sachverhalte) und die erwarteten Ausgaben des Systems (hier z.B. Rechtsfolgen), und für jeden Testfall wird dann geprüft, ob die erwarteten Ausgaben (die Kontrollausgabe) der tatsächlichen Ausgabe des Systems entsprechen. Die Wahl der Testfälle in der Testdatenbank legt fest, welches Kriterien aus Abschnitt 4 überprüft werden: Sind in der Testdatenbank Testfälle enthalten, die vorsätzlich widersprüchliche Informationen enthalten, so kann die Robustheit (Plausibilität) oder auch die Erfüllung der Zweckbestimmung (Adäquatheit) des Systems getestet werden; mit repräsentativen (nicht-widersprüchlichen) Testdaten kann die Genauigkeit des Systems (Korrektheit, Vollständigkeit, Redundanz), und die Erfüllung der Zweckbestimmung (Effizienz/Effektivität) getestet werden. Ebenso können viele der anderen Kriterien durch eine passende Auswahl von Testdaten überprüft werden.

Der Testaufbau aus Abb. 1 kann auch umgekehrt genutzt werden: Fixiert man Testfälle und die Deduktionsmaschine M und betrachtet die formalisierten Normen als Subjekt des Testverfahrens, so kann die Adäquatheit der Normen gegenüber vorher festgelegten Fällen (und deren erwarteten Rechtsfolgen) untersucht werden. Dies könnte z.B. für sog. legal drafting genutzt werden.

Als Fazit lässt sich festhalten, dass der KI-VO-E richtigerweise auch rechtliche Voraussetzungen für die Beurteilung der Qualität auch von symbolischen KI-Verfahren festschreibt, obwohl diese Verfahren üblicherweise im Gegensatz zu subsymbolischen Verfahren, die als “Black-Box” gesehen werden, als logik-basierte Systeme unverdächtig und transparent angesehen werden. Die Auslegung der Rechtsnormen ist dabei besonders komplex, da diese die verschiedensten technischen Verfahren zu berücksichtigen hat. Auslegungsergebnisse für subsymbolische sind dabei sicher nicht auf symbolische KI-Verfahren übertragbar; es sind noch nicht einmal ohne weiteres die hier vorgestellten Auslegungsergebnisse für Deduktionsmaschinen auf andere symbolische Verfahren anwendbar.

Die Komplexität der juristischen Auslegungsaufgabe wird in Zukunft noch weiter zunehmen, da Systeme wie J vermehrt als hybride KI-Systeme entworfen werden, also als Kombination von symbolischen und subsymbolischen Verfahren. Hierfür sind, soweit ersichtlich, keine spezifischen Auslegungskonzepte entwickelt worden, oder gar entsprechende Normen im KI-VO-E enthalten.