1.
Einleitung ^
[1]
In Österreich wird im Rahmen des eGovernments und in anderen Bereichen das sogenannte bereichsspezifische Personenkennzeichen (bPK) eingesetzt, welches ein eindeutiges, von der Nummer der Eintragung im Zentralen Melderegister (ZMR-Zahl) abgeleitetes Pseudonym für eine natürliche Person darstellt (bzw. darstellen soll). Für die folgende Analyse der bereichsspezifischen Personenkennzeichen sind folgende Definitionen und Aussagen des E-Government-Gesetzes relevant:
- Eindeutige Identität: Die Bezeichnung der Nämlichkeit eines Betroffenen (Z 7) durch ein oder mehrere Merkmale, wodurch die unverwechselbare Unterscheidung von allen anderen bewirkt wird [EGovG, § 2 Z 2].
- Stammzahl: Eine zur Identifikation von natürlichen und juristischen Personen und sonstigen Betroffenen herangezogene Zahl, die demjenigen, der identifiziert werden soll, eindeutig zugeordnet ist und hinsichtlich natürlicher Personen auch als Ausgangspunkt für die Ableitung von (wirtschafts-)bereichsspezifischen Personenkennzeichen (§§ 9 und 14) benützt wird [EGovG, § 2 Z 8]. Für natürliche Personen, die im Zentralen Melderegister einzutragen sind, wird die Stammzahl durch eine mit starker Verschlüsselung gesicherte Ableitung aus ihrer ZMR-Zahl (§ 16 Abs. 1 des Meldegesetzes 1991, BGBl. Nr. 9/1992) gebildet. Für alle anderen natürlichen Personen ist ihre Ordnungsnummer im Ergänzungsregister (Abs. 4) für die Ableitung der Stammzahl heranzuziehen [EGovG, § 6 (2)].
- Das bereichsspezifische Personenkennzeichen wird durch eine Ableitung aus der Stammzahl der betroffenen natürlichen Person gebildet. Die Identifikationsfunktion dieser Ableitung ist auf jenen staatlichen Tätigkeitsbereich beschränkt, dem die Datenanwendung zuzurechnen ist, in der das Personenkennzeichen verwendet werden soll (bereichsspezifisches Personenkennzeichen, bPK) [EGovG, § 9 (1)]. Die zur Bildung des bPK eingesetzten mathematischen Verfahren (Hash-Verfahren über die Stammzahl und die Bereichskennung) werden von der Stammzahlenregisterbehörde festgelegt [EGovG, §9 (3)].
[2]
Im Detail (siehe [Hollosi 2007]) werden Stammzahl und bereichsspezifisches Personenkennzeichen wie unten beschrieben berechnet. Grob betrachtet, wird zunächst aus einer eindeutigen personenbezogenen Basiszahl eine Stammzahl abgeleitet. Davon ausgehend wird (unter Einbeziehung einer Bereichskennung) das bereichsspezifische Personenkennzeichen (bPK) berechnet (siehe Abbildung 1).
1.1.
Berechnung der Stammzahl S ^
[3]
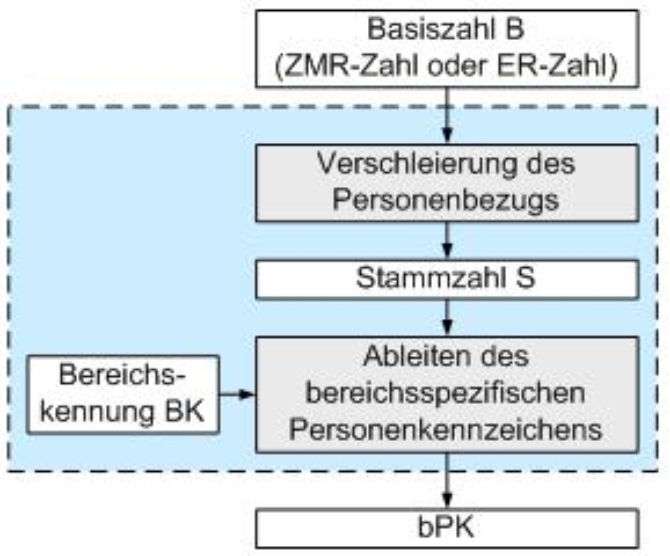
Die Stammzahl S wird aus datenschutzrechtlichen Gründen mittels einer Einwegfunktion aus der sogenannten Basiszahl B abgeleitet. Die Basiszahl ist für jede in Österreich lebende natürliche Person eindeutig. Für in Österreich meldepflichtige Personen wird die ZMR-Zahl als Basiszahl herangezogen, für alle anderen die Zahl der Eintragung im Ergänzungsregister (ER-Zahl). Die Berechnung der Stammzahl S aus der Basiszahl B erfolgt in fünf Schritten:
- Ausgangsdaten: Basiszahl B (12 Dezimalstellen)
- Binärcodierung der Basiszahl (5 byte)
- Verlängern auf 128 bit (16 byte) mittels folgendem Format: b = B || seed || B || B, wobei seed ein geheimer, konstanter 8-bit-Wert ist, der nur der Stammzahlregisterbehörde bekannt ist.
- Verschlüsseln der binären Repräsentation b mittels 3DES im CBC-Modus, wobei der verwendete geheime Schlüssel wiederum nur der Stammzahlregisterbehörde bekannt ist.
- Die base64-Codierung des Ergebnisses ist die Stammzahl S.
[4]
Analyse: Stammzahlen sind zwingend eindeutig, weil die Basiszahlen eindeutig sind, und der oben beschriebene Ansatz eine Blockchiffre mit systemweit konstantem Schlüssel (und systemweit konstanter Seed) verwendet. Geraten diese Daten, insbesondere der 3DES-Schlüssel an die Öffentlichkeit, so ist jede Stammzahl auf die ZMR-Zahl (bzw. ER-Zahl) und damit auf die zugeordnete Person rückführbar. Im Falle der Kompromittierung des Schlüssels müsste ein neuer Schlüssel ausgegeben werden, was eine Neuberechnung aller bisher verwendeten Stammzahlen und der aus ihnen abgeleiteten bereichsspezifischen Personenkennzeichen zur Folge hätte. Letzteres ist aufgrund der Einwegcharakteristik der Ableitungsfunktion (siehe Abschnitt 1.2) unmöglich.
1.2.
Berechnung des bereichsspezifischen Personenkennzeichens bPK ^
[5]
Bereichsspezifische Personenkennzeichen (bPK) sollen verhindern, dass Daten aus unterschiedlichen Bereichen zusammengeführt (d.h. miteinander verknüpft) werden können. Hierzu fließt in die Berechnung des bPK neben der Stammzahl eine (eindeutige) Bereichskennung BK ein, die den Bereich, in dem dieses Personenkennzeichen genutzt werden soll, repräsentiert. Um nicht Datensätze unterschiedlicher Personen unter demselben bPK abzulegen, sollte dieses mit hoher Wahrscheinlichkeit eindeutig sein.
- Ausgangsdaten: Stammzahl (base64-codiert) und Bereichskennung (ISO-8859-1 Zeichenfolge der Abkürzung des Bereiches laut E-Government-Bereichsabgrenzungsverordnung [E-Gov-BerAbgrV] in der Regel 2, maximal 5 Zeichen in Großbuchstaben)
- Konkatenation von Stammzahl S und Bereichskennung BK zu einer Zeichenkette: S || “+“ || URN-Präfix || BK, wobei der URN-Präfix “urn:publicid:gv.at:cdid+“ verwendet wird.
- Berechnung des SHA-1-Hashwertes der Zeichenkette (160 bit) [NIST 1995].
- Der Hashwert wird entweder direkt als bPK genutzt oder vor Übertragung (bzw. Ausdruck) base64-codiert.
[6]
Analyse: Aufgrund des Einsatzes einer Hashfunktion in Schritt 3 kann ein gegebenes bereichsspezifisches Personenkennzeichen nicht auf seine Ursprungsdaten (d.h. die Stammzahl) zurückgeführt werden. Die bereichsspezifischen Personenkennzeichen haben eine Länge von 160 bit, sind aber aufgrund der eingesetzten Hashfunktion nicht zwingend eindeutig. Dies bringt unweigerlich die Gefahr von Dubletten und nicht mehr separierbaren Einträgen in Datenbeständen des eGovernments und weiteren Bereichen mit sich.
2.
Garantiert eindeutige bereichsspezifische Personenkennzeichen ^
[7]
Das in [Schartner 2012a] beschriebene Konzept für eindeutige aber dennoch unverknüpfbare Identifier (die so genannten Collision-Free Numbers – CFNs) und die zugehörigen Generatoren (Collision-Free Number Generators – CFNGs) können verwendet werden, um die beiden oben diskutierten Schwächen der bestehenden bereichsspezifischen Personenkennzeichen (systemweite Geheimnisse und Gefahr von Dubletten) zu beheben.
[8]
Die Berechnung des bPK kann durch den in Abbildung 2 dargestellten CFNG ersetzt werden. Dessen Output ist bei einer Länge von 160 bit garantiert systemweit eindeutig, aber dennoch nicht auf die Stammzahl rückführbar. Die gesetzlichen Forderungen nach Eindeutigkeit, Bereichstrennung und Identitätsschutz werden daher durch die Nutzung von CFNGs in vollem Umfang erfüllt.
[9]
Detaillierte Beweise für die Sicherheit des CFNG-Verfahrens, die Eindeutigkeit und Unverknüpfbarkeit der erzeugten Werte und weitere Anwendungsszenarien sind [Schartner 2012a] zu entnehmen.
[10]
Im Detail muss der CFNG wie folgt parametrisiert werden (siehe auch [Schartner 2012b]):
- Da die ZMR- bzw. die Basiszahl nicht direkt genutzt werden darf, wird wiederum die eindeutige Stammzahl S (128 bit) als Basis-Identifier herangezogen.
- Neben der Stammzahl S muss auch die Bereichskennung BK in die Berechnung des bPK einfließen.
- Da die Bereichskennung BK aus maximal 5 Großbuchstaben besteht, kann sie mittels log2(265) = 24 bit codiert werden.
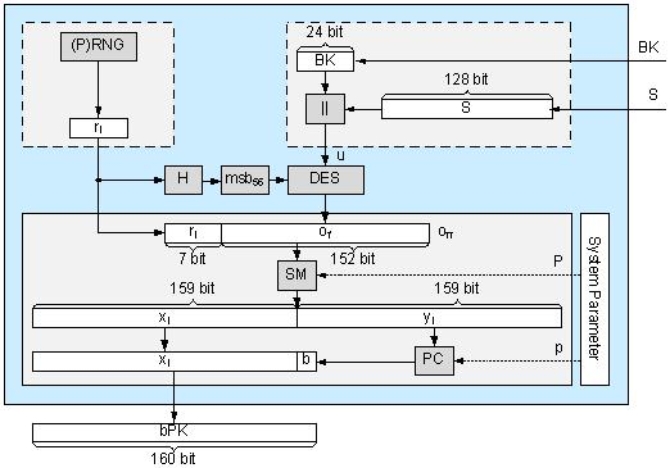
- Zieht man von 160 bit das Bit b für die Codierung der y-Koordinate, 24 bit für die codierte Stammzahl und 128 bit für die Stammzahl ab, so bleiben 7 bit, welche für einen Randomizer r genutzt werden können. Der Randomizer wird wahlweise durch einen echten Zufallsgenerator (Random Number Generator – RNG) oder einen Generator für pseudozufällige Zahlen (Pseudo-Random Number Generator – PRNG) für jeden Ableitungsvorgang frisch erzeugt.
- Das bereichsspezifische Personenkennzeichen wird somit wie folgt berechnet: bPK = PC(SM(DESk(S||BK)||r)) mit |r| = 7 und k = msb56(H(r)), wobei zunächst zur Verschlüsselung der DES (Data Encryption Standard) genutzt wird und abschließend die ECC-Skalar-Multiplikation SM (mit einem systemweit fixen Punkt P) und anschließender Point-Compression PC durchgeführt wird. Details zu den verwendeten kryptographischen Mechanismen sind in [Menezes 1996] und [Hankerson 2004] zu finden.
[11]
Dabei ist k = msb56(H(r)) die Verlängerung des 7 bit langen Randomizers auf die Schlüssellänge von DES: Nach Hashen des Randomizers mit einer Hashfunktion H (wie SHA-1 [NIST 1995] oder RIPEMD160 [Dobbertin 1996]) werden die höchstwertigsten 56 bit als Schlüssel genutzt. Die geringe Entropie des Schlüssels („nur“ 128 Möglichkeiten) stellt hierbei kein Sicherheitsproblem dar, weil die Verschlüsselung nur die Brute-Force-Suche erschweren soll, falls Teile von S bekannt sind, oder, bezogen auf einen bestimmten Bereich, der Wert BK fest ist.
2.1.
Alternative 1: kompaktere Codierung der Bereichskennzeichen ^
[12]
Derzeit sind laut der Anlage zu § 3 Abs. 1 der E-Government-Bereichsabgrenzungsverordnung [E-Gov-BerAbgrV] nur 35 Bereichskennungen (Teil 1 enthält 26, Teil 2 enthält 9) spezifiziert. Der theoretische Maximalwert von 24 bit (maximal 5 Großbuchstaben) lässt sich daher zugunsten der Länge des Randomizers auf einen praktisch sinnvollen Wert (z.B. 12 bit, d.h. maximal 212 = 4096 unterschiedliche Bereichskennungen) reduzieren. Die Binärcodierung der einzelnen Bereichskennungen wäre dementsprechend in der Anlage der Verordnung zu ergänzen. Für den Randomizer stehen nun 19 bit zur Verfügung. Der Mehraufwand bei einem Angriff mittels Brute-Force erhöht sich somit um den Faktor 212= 4096 (von 27 = 128 auf 219 = 524288).
2.2.
Alternative 2: Direkte Nutzung der Basiszahl B (gesetzlich in Österreich nicht zulässig) ^
[13]
Diese Variante benutzt an Stelle der Stammzahl S (128 bit) direkt die Basiszahl B (5 byte = 40 bit) und verkürzt somit den Input der Verschlüsselungsfunktion um 88 bit. Nutzen wir statt DES den Skipjack-Algorithmus [NIST 1998] (Blocklänge 64 bit, Schlüssellänge 80 bit, CBC-Mode mit ciphertext stealing) so können nun 80 bit für den Randomizer und 15 bit für die Codierung zusätzlicher Informationen (X) verwendet werden. In diesem Datenblock kann beispielsweise ein Zähler enthalten sein, sodass eine Person in ein und demselben Bereich unterschiedliche Pseudonyme zur Verfügung stehen. Die unverknüpfbaren eindeutigen Pseudonyme sind nun von der Form bPK = PC(SM((SJr(B || X || BK) || r), P)), wobei |B| = 40 bit, |X| = 15 bit, |BK| = 24 bit und |k| = 80 bit sind.
[14]
Anmerkung: Da diese Variante die Stammzahl nicht benötigt, ist sie auch nicht mehr von der Geheimhaltung des bei der Ableitung der Stammzahlt genutzten Schlüssels (siehe Abschnitt 1.1) abhängig. Es ist allerdings zu beachten, dass die direkte Nutzung der Basiszahl, welche in anderen Anwendungsgebieten auch durch die Nummer des Reisepasses oder die Sozialversicherungsnummer ersetzt werden kann, (zumindest) in Österreich gesetzlich untersagt ist. In diesen Fällen ist das ursprüngliche Konzept oder die Variante 1 zu verwenden.
2.3.
Wirtschaftsbereichsspezifische Personenkennzeichen ^
[15]
Da der Algorithmus zur Bestimmung des wirtschaftsbereichsspezifischen Personenkennzeichens (wbPK) abgesehen von geänderten Inputdaten analog zum Algorithmus des bPK ist, kann im Prinzip die in Abschnitt 2 skizzierte Vorgehensweise gewählt werden, um auch im Kontext der wbPKs Dubletten zu vermeiden.
[16]
Anmerkung: Da nun aber die base64-codierte Stammzahl der natürlichen Person und die Stammzahl des Auftraggebers als Bereichskennung in die Berechnung einfließen, können Dubletten nur vermieden werden, wenn die Begrenzung der wbPKs auf 160 bit aufgehoben wird.
3.
Zusammenfassung ^
[17]
Bei dem derzeit spezifizierten und benutzten bereichsspezifischen Personenkennzeichen (bPK) ist eine eindeutige Zuordnung zwischen der Basiszahl B des Inhabers und dem bPK nicht hundertprozentig garantiert. Die gesetzliche Forderung “mit hoher Wahrscheinlichkeit eindeutig“ ist zwar erfüllt, aber technisch könnte man diese Wahrscheinlichkeit für das Auftreten von Dubletten mit dem oben beschriebenen Ansatz auf null reduzieren. Weitere Anwendungsszenarien für das skizzierte Prinzip (wie digitale Pseudonyme oder eindeutige Schlüsselkomponenten im Kontext qualifizierter elektronischer Signaturen [SigG, SigV]) sind in [Schartner 2012a] zu finden.
4.
Literatur ^
Dobbertin H., Bosselaers, A., Preneel, B.: RIPEMD-160: A Strengthened Version of RIPEMD, in Gollmann, D.: Proceedings of Fast Software Encryption (FSE), Springer-Verlag, S. 71-82, (1996).
EGovG: Bundesgesetz über Regelungen zur Erleichterung des elektronischen Verkehrs mit öffentlichen Stellen (E-Government-Gesetz - E-GovG), StF: BGBl. I Nr. 10/2004 (Fassung vom 15.1.2012).
E-Gov-BerAbgrV: Verordnung des Bundeskanzlers, mit der staatliche Tätigkeitsbereiche für Zwecke der Identifikation in E-Government-Kommunikationen abgegrenzt werden (E-Government-Bereichsabgrenzungsverordnung – E-Gov-BerAbgrV), StF: BGBl. II Nr. 289/2004 (Fassung vom 15.1.2012).
Hankerson, D., Menezes, A.J., Vanstone, S.A.: Guide to Elliptic Curve Cryptography, Springer-Verlag (2004).
Hollosi, A., Hörbe, R.: Bildung von Stammzahl und bereichsspezifischem Personenkennzeichen (bPK), Bundeskanzleramt Österreich, Stabstelle IKT-Strategie des Bundes (SZ-bPK-Algo V1.1.1) (2007).
Menezes, A.J., Vanstone, S.A., Van Oorschot, P.C.: Handbook of Applied Cryptography, CRC Press (1996).
National Institute of Standards and Technology (NIST): SKIPJACK and KEA Algorithm Specifications, ver. 2 (1998).
National Institute of Standards and Technology (NIST): FIPS Publication 180-1: Secure Hash Standard (SHA) (1995).
Schartner, P.: Random but system-wide unique unlinkable Parameters, JIS – Journal of Information Security, Vol.3, No.1, Jänner 2012, ISSN Print: 2153-1234, ISSN Online: 2153-1242, (http://www.scirp.org/journal/jis, DOI: 10.4236/jis.2012.31001) (2012a).
Schartner, P.: Unique Domain-Specific Citizen Identification for E-Government Applications, In Proceedings of “The 6th International Conference on Digital Society 2012 (ICDS)”, 30 Jänner – 4 Februar 2012, Valencia, Spanien, in Druck (2012b).
SigG: Bundesgesetz über elektronische Signaturen (Signaturgesetz – SigG), StF: BGBl. I Nr. 190/1999 (Fassung vom 15.1.2012).
SigV: Verordnung des Bundeskanzlers über elektronische Signaturen (Signaturverordnung 2008 – SigV 2008), StF: BGBl. II Nr. 3/2008 (Fassung vom 15.1.2012).
