Jusletter IT

Die Verwendung von graphischen Notationen¹ zur übersichtlicheren und schnelleren Erfassung von Geschäftsprozessen, und teils auch als Ausgangslage für einen Transfer in ein automatisiertes Verfahren, ist gängige Praxis sowohl im Unternehmensumfeld wie auch in der öffentlichen Verwaltung. So ist Geschäftsprozessmodellierung im Entwurf des derzeit im Gesetzgebungsverfahren befindlichen E-Governmentgesetzes fest verankert [vgl. Art.1 §9 ].

In den letzten Jahren hat unter den diversen im Einsatz befindlichen Notationen die BPMN²-Notation eine zunehmende Verbreitung erfahren [Freund & Rücker, XII, Abb. 1]. Dies wird auch daran sichtbar, dass immer mehr Anbieter professioneller Geschäftsprozessmanagementsoftware BPMN in ihren Leistungsumfang aufgenommen haben. Das hat dazu geführt, dass BPMN auch in der öffentlichen Verwaltung immer stärker wahrgenommen wird. Dies verwundert nicht, gibt es doch insbesondere auf Bundesebene in Deutschland deutliche Anstöße, über Ländergrenzen hinweg voneinander anhand von Prozessmodellen zu lernen. Da ist Neugier auf einen sich zunehmend verbreiteten Standard, der solche Vergleiche möglicherweise vereinfachen würde, nicht ungewöhnlich.

Diverse Rückmeldungen aus der Verwaltungspraxis an die Autorin deuten hingegen darauf hin, dass BPMN für die fachliche Modellierung als zu kompliziert empfunden wird³. Dies rückt einen eigentlich selbstverständlichen Aspekt von Notationen in den Vordergrund, der insbesondere im Zusammenhang mit der oben angedeuteten Zielsetzung steht, unterschiedliche Prozesslösungen leicht vergleichen zu können: Prozessmodellierungsnotationen dienen nicht nur der Fixierung von Prozessen und als Voraussetzung oder Unterstützung, für diese Prozesse IT-Lösungen zu generieren. Sie sollen ebenso ein schnelles menschliches Erfassen der Prozesse ermöglichen und als Beschreibungshilfe zu den Prozessen oder als Verständigungsbasis für Gespräche, Vergleiche und Analysen zu den aufgezeichneten Prozessen dienen. Sie haben daher eine nicht unwesentliche sprachliche Komponente. Abstraktionen sollen hier Verständnis erleichtern, nicht erschweren!

Werden Prozessmodelle im Vorfeld einer Applikationsentwicklung konzipiert, so dienen sie im Allgemeinen der Verständigung zwischen unterschiedlichen Organisationseinheiten einer Institution.⁴ Fachlich involvierte Prozessbeteiligte müssen sie genauso verstehen können wie die mit Systemanalyse an den IT-Lösungen befassten Beschäftigten. Die jeweiligen Erfahrungswelten mit dem Umgang formalisierter Darstellungen sind jedoch i. d. R. völlig verschieden. Und je nach Zielsetzung werden Prozessmodelle auch Beschäftigten auf der Umsetzungsebene im Sinne von Handlungsanweisungen bzw. zur Vorgehensunterstützung zur Verfügung gestellt. Führungskräfte können die Modelle zur Aufgabensteuerung heranziehen.

Die Entwicklung der Nationalen Prozessbibliothek in Deutschland zeigt, dass sogar länder-, ressort- und organisationsübergreifende Verständigungen gewünscht sind. Bereits vorhandene Lösungen sollen aufgegriffen und Mehrfachentwicklungen vermieden werden. Ebenso sollen Lösungen für Prozessketten gefunden werden, die eine Zusammenarbeit über mehrere Institutionen hinweg erfordern. Inwieweit diese Ansinnen realistisch sind, sei dahingestellt. Zweifellos wäre eine organisatorische Vorgabe zur Verwendung einer einheitlichen Notation für solche Zwecke hilfreich. Doch ähnlich, wie es möglich ist, innerhalb der deutschen Sprache, kurze und knappe, oder auch fürchterlich lange, verschachtelte, dann fast nicht mehr verständliche Sätze zu gestalten, so ist es selbst bei Verwendung der gleichen Notation möglich, sehr unterschiedliche Darstellungen zu finden. Somit wären auch dann noch weitere Festlegungen, nämlich Modellierungsstandards, zwingend. Dies würde zumindest gelten, wenn ein schnelles Durchforsten und Vergleichen der national gesammelten Prozesse zum Zwecke effizienterer öffentlicher Lösungsfindungen nicht nur einem kleinen Kreis mit Spezialkenntnissen möglich sein sollte.

Wer mit Prozessmodellen möglichst breite Wirkung erzeugen möchte, sollte sich den sprachlichen Aspekt von Modellierungsnotationen daher immer wieder in den Vordergrund rufen und entsprechend organisationsübergreifende Regelungen treffen. Bundes- oder landesweit und insbesondere auf kommunaler Ebene wären die Vorgabe einer Notation sowie von Standards oder aber zumindest Empfehlungen hierzu hilfreich. Dazu ist anzumerken, dass hiermit keineswegs das Wettbewerbsrecht ausgehebelt würde. Etliche Notationen werden von verschiedenen Firmen unterstützt. Eine entsprechende organisatorische Vorgabe ist insbesondere deshalb von Bedeutung, weil vorhandene Notationen einander oft nicht äquivalent sind: es ist i. d. R. nicht möglich, einfach, d. h. automatisiert, von einer Notation in eine andere zu transformieren.

Bei der Wahl einer Notation sind diverse Aspekte zu beachten. Eine gute Notation muss ausdrucksstark genug für die damit beabsichtigten Ziele sein und sollte leicht erlernbar, leicht verständlich bzw. schnell erfassbar sowie möglichst weit verbreitet sein.

Dabei gibt es natürlich Überschneidungen zwischen diesen Eigenschaften. Eine leicht erlernbare Notation wird zumeist auch schnell erfassbar und leicht verständlich sein. Dies in Verbindung mit einer guten Ausdrucksstärke ist sicherlich ein Einflussfaktor für eine weite Verbreitung. Hingegen kann große Ausdrucksstärke schnellem Erfassen und leichter Verständlichkeit entgegenstehen.

Wir haben uns daran gewöhnt, dass durch Abstraktionen bzw. Modellbildung Informationen verloren gehen, weil wir bestimmte Blickwinkel in den Vordergrund rücken und Aspekte, die hierfür irrelevant sind, weglassen. Genau hierin kann begründet sein, dass die Abstraktion schneller und leichter verständlich ist als die Ausgangssituation. Informationsverluste kann es aber auch geben, wenn man auf (zumindest scheinbar) ein und derselben Abstraktionsstufe zwischen verschiedenen Darstellungen wechselt. Hierzu kann man Notationen und lebende Sprachen gut vergleichen. Oft unterscheiden sich Notationen wie auch lebende Sprachen hinsichtlich des «Sprachumfangs» bzw. in ihrer Ausdrucksstärke. Dann ist eine «Übersetzung» nicht umkehrbar eindeutig möglich. Es können beim Transfer Informationen verloren gehen oder Informationen zur korrekten Darstellung fehlen. Eine weitere Analogie zu natürlichen Sprachen besitzen Notationen darin, dass sie in der Regel leichter zu erlernen sind, wenn man bereits andere beherrscht.

In der jungen Wissenschaft der Informatik ist innerhalb der Theoretischen Informatik die Auseinandersetzung mit prinzipiell von Maschinen lesbaren, so genannten formalen Sprachen und deren Ausdrucksfähigkeit ein klassisches Lehrgebiet [Asteroth & Baier, Seite 11]. Allerdings untersucht die Theoretische Informatik nicht, welche Sprache besonders «menschenfreundlich», also aus menschlicher Sicht besonders verständlich, leicht erlern- und anwendbar ist, sondern klassifiziert Sprachen nach ihren Einsatzmöglichkeiten auf Computern, sucht nach Grenzen ihrer Ausdrucks- oder Transferfähigkeit. Dies beinhaltet Fragen danach, welche Probleme mit welchen formalen Sprachen mit welchem Aufwand gelöst werden können. Demgegenüber werden in der Praktischen Informatik unter anderem Werkzeuge entwickelt, die den Transfer von einer Sprach(ebene) in eine andere unterstützen. Auf beides wird im Folgenden näher eingegangen.

Die Theoretische Informatik befasst sich u. a. mit so genannten Formalen Sprachen [Rechenberg, Seite 180 ff.]. Diese lassen sich im Gegensatz zu Natürlichen Sprachen klar abgrenzen. So muss stets überprüfbar sein, ob ein vorgegebenes Wort oder ein vorgegebener Satz – beides aus Sicht der Informatik Zeichenfolgen und somit gleichermaßen Worte – der Sprache angehört. Dazu wird der Sprachumfang exakt definiert. Eine Möglichkeit besteht darin, die Menge der Worte, die zur Sprache gehören, genau anzugeben. Eine andere besteht darin, einen zulässigen Zeichenvorrat, das Alphabet, und hierauf geltende Regeln, die so genannte Grammatik, zu definieren. Aus diesen Vorgaben lässt sich dann die Sprache erzeugen. Beide Vorgehensweisen sichern eine syntaktische Prüfung.

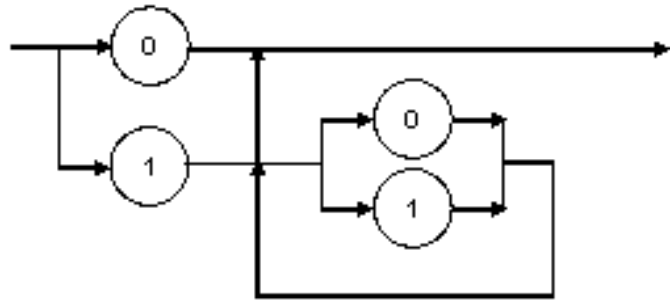
So ist die Menge {P, müde, Ist P müde?} in diesem Sinne nach dem ersten Vorgehen eine formale Sprache. Ein sukzessiver Vergleich mit den Elementen der Menge gibt Gewissheit, ob eine gegebene Zeichenkette der Sprache angehört. «A» und «P ist müde.» etwa gehören nicht zu dieser Sprache, «müde» sowie, «Ist P müde?» schon. Entlang der zweiten Möglichkeit könnte das Alphabet {0,1} lauten und die Grammatik besagen, dass die 0 zugelassen ist und ansonsten jede Folge von Zeichen aus den Binärziffern, die nicht mit 0 beginnt. Dann wären 0 sowie 10010010 zulässige Zeichenfolgen dieser Sprache, nicht jedoch 001.

Etwas exakter lässt sich eine formale Sprache wie folgt definieren. Man benötigt eine endliche Menge Σ an Zeichen, die in der Sprache vorkommen dürfen, das Terminalalphabet. Im Beispiel wäre Σ = {0,1}. Darüber hinaus wird eine weitere endliche Menge V benötigt, das Nichtterminalalphabet. Die hierin enthaltenen Zeichen symbolisieren Variablen für Worte, die aus Zeichen des Alphabets Σ gebildet werden können. Darüber hinaus dürfen sie auch für das leere Wort stehen. Um Verwechslungen zu verhindern, müssen Zeichen aus dem Terminalalphabet von denen des Nichtterminalalphabets abweichen: Σ ∩ V = ∅. Ferner gibt es ein Startsymbol S ∈ V und eine endliche Regelmenge P, die Produktionen. Diese lassen sich als Mengen von Tupeln, links das Startwort, rechts das Zielwort ebenso in Mengenschreibweise definieren. Hierauf wird an dieser Stelle verzichtet. «Die einzige Forderung ist, dass das Wort auf der linken Seite einer Regel mindestens ein Nichtterminal enthält» [Asterroth & Bayer (2002) ,197]. Die von einer solchen Grammatik erzeugte Sprache besteht aus allen Wörtern, die sich aus dem Startsymbol durch Anwenden der Regeln ableiten lassen.

Folgende Ausführungen zum obigen Beispiel verdeutlichen das Vorgehen. So ist hier Σ = {0,1}. Es sei V = {S, A, B}. Die Regelmenge {(S, 0), (S, 1A), (A , ε), (A, B), (A, AB), (B,0), (B,1) } erzeugt die gewünschten Binärzahlen, wobei mit ε das leere Wort gemeint ist. In Tabelle 1 sind die Regeln in einer etwas leichter lesbaren Form dargestellt. Der senkrechte Strich deutet eine Alternative an.

Tabelle 1: Produktionen zum Beispiel Dualzahlen ohne führende Nullen

Durch Anwenden der Regeln wird deutlich, dass sich die gewünschten Dualzahlen ableiten lassen. Sà0 führt direkt zu 0. Sà1Aà1e  liefert die 1. Weiter führt Sà1Aà1ABà1A0 bzw. zu 1A1. Es lässt sich also jede Dualzahl bilden, die mit 1 beginnt und mit 0 oder 1 endet, denn der Mittelteil A kann wieder zu 0 bzw. 1 aufgelöst werden und dies durch die AB-Regel beliebig oft⁵.

Die Bildung von Dualzahlen ließe sich genauso gut mit einem Syntaxdiagramm beschreiben, wie Abbildung 1 zeigt. Das Syntaxdiagramm darf von links nach rechts entlang der dargestellten Pfeile durchlaufen werden und beim Passieren der Symbole 0 bzw. 1 werden diese sukzessive niedergeschrieben.

Abbildung 1: Syntaxdiagramm Dualzahl ohne führende Nullen (eigene Abbildung)

Die Dualzahlen 0, 10 und 11 lassen sich über die Regeln (1) und (3) herleiten oder aber, indem man im Diagramm den obersten Pfad durchläuft (0) bzw. den unteren Pfad betritt und dann im einen Fall den oberen (10), im anderen Fall den unteren Weg (11) durch die weiter folgenden Binärziffern wählt und nach dem Zurückgehen das Diagramm verlässt.

Der Theoretischen Informatik haben wir eine Klassifizierung der formalen Sprachen zu verdanken. Sprachen, zu denen man eine Regelmenge finden kann, bei denen auf der linken Seite nur Nichtterminalsymbole stehen – das war in dem gewählten Beispiel der Dualzahlbildung der Fall – heißen regulär. Sie lassen sich stets auch in Form eines Syntaxdiagramms darstellen [vgl. Asteroth & Baier, Seite 257 ff.] und eine Überprüfung, ob ein Wort einer solchen Sprache angehört ist recht effizient möglich. Auch Notationen mit ihrem Symbolvorrat und den dazu gehörigen Verwendungsregelkönnen als formale Sprachen verstanden werden.⁶ Hierauf basieren auch die von etlichen Modellierungstools vorgesehenen Möglichkeiten, syntaktische Fehler in den Modellierungen zu entdecken.

Dies ist vergleichbar mit der Umwandlung von Programmbefehlen in Maschinensprache. Hier ist eine erste lexikalische und Syntaxprüfung stets erforderlich [Asteroth & Baier, Seite 11, 193]. Inwieweit die erstellten Befehle jedoch auch «sinnvoll», d. h. semantisch korrekt sind und zur Lösung des Problems führen, das durch das Programm bewältigt werden soll, bleibt hierbei offen. Dies ist Personen, die programmieren, geläufig. Auch wenn ein Programm den Compilierungsvorgang fehlerfrei überstanden hat, kann es dennoch sein, dass dessen Ergebnisse nicht korrekt sind oder, mindestens ebenso ärgerlich, dass das Programm nicht terminiert.

Für ein menschliches Verstehen der Prozessmodelle ist deren Zuordnung zu einer Klasse formaler Sprachen jedoch überhaupt nicht von Bedeutung. Im Gegenteil. Vielleicht ist eine Regelmenge, die besonders anschauliche Diagramme ermöglicht, sich aber nicht gleich einer bestimmten Klasse formaler Sprachen zuordnen lässt, viel besser geeignet. Auch Anreicherungen der Modelle um zusätzliche Informationen, die mit den theoretischen Sprachkonzepten zunächst nicht in Einklang stehen, können zweckmäßig sein.

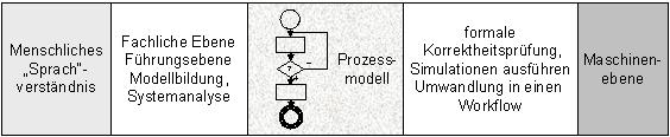
In diesem Fall sollte im Vordergrund stehen, für den jeweiligen Anwendungszweck eine möglichst anschauliche Darstellung zu ermöglichen. Andererseits würde man danach trachten, dennoch formale Korrektheitsüberprüfungen zu ermöglichen, etwa indem man intern unsichtbare Umwandlungen des Modells in besser überprüfbare Anordnungen vornehmen ließe.⁷ Wiederum andere Anforderungen würden entstehen, wenn man zugleich eine automatische Workflowgenerierung des Prozesses im Sinn hat. Hier muss dann ein Transfer des Modells in einen Programmcode erfolgen.

Mit Transformationen befasst sich wiederum die Praktische Informatik. So gehört in dieses Gebiet die Entwicklung höherer Programmiersprachen, zu denen stets ein Übersetzungsprogramm in Maschinensprache gehört. Ebenfalls werden hier Lösungen mit unterschiedlichen Sichten für verschiedene Nutzergruppen (Rollen) entwickelt.

Wie im einführenden Abschnitt bereits bemerkt, müssen Prozessmodelle verschiedene Sprach- und somit Abstraktionsstufen abdecken (vgl. Abb. 2). Führungsebene, Sachbearbeitung, Systementwicklung wurden bereits genannt. Bei dem Wunsch nach Korrektheitsprüfung und Workflowgenerierung, oder wenn Simulationen möglich sein sollen, muss das Prozessmodell maschinell lesbar sein.

Abbildung 2: Ebenen, die mit einem Prozessmodell erreicht werden sollen (eigene Abbildung)

Und noch gar nicht betrachtet wurden Anforderungen, die entstehen, wenn man aufgrund der verschiedenen praktisch genutzten Notationen verschiedene Darstellungsformen lesend und schreibend unterstützen möchte. Dies ist ohne Verluste nur dann lösbar, wenn die Ausdrucksfähigkeit der Sprachen gleich ist.

Insgesamt sind die Ansprüche an die verschiedenen Ebenen so unterschiedlich, dass es zweckmäßig erscheint, unterschiedliche Sichten auf die Modelle zu generieren. Dies wird auch von etlichen Werkzeugen angeboten. So liefern aggregierte Modelle für Führungskräfte auf einer abstrakteren Ebene schneller die hier erforderlichen Informationen und für eine Systemanalyse ist das Einblenden weiterer zusätzlicher Informationen, die auf der fachlichen Ebene nicht sichtbar sind, von Vorteil.

Nicht unbeachtet bleiben sollte darüber hinaus, dass auch individuelle Unterschiede das Verständnis im Ungang mit Abstraktionen beeinflussen. Auch dieser, hier als «Erfahrungswissen» bezeichnete Aspekt, hat Einfluss darauf, wie gut das Lesen oder Entwickeln von Prozessmodellen funktioniert.

Individuelle Unterschiede spielen in allen Lebensbereichen eine wesentliche Rolle. Im Idealfall haben daher gute Applikationen generell nicht nur ggf. erforderliche rollenspezifische Sichten, sondern auch individuelle Anpassungsmöglichkeiten. Allerdings besteht hier noch großer Entwicklungsbedarf. Noch passt sich der Mensch mehr der Maschine an als umgekehrt. Wäre es bereits anders und könnte man durch Computerprogramme zwischen all diesen Abstraktionsebenen ohne Informationsverluste hin und her zu springen, dann wäre das Problem, künstliche Intelligenz zu erzeugen, gelöst [vgl. Hofstadter (1985), u. a. Seite 608 ff.].

Notationen sind Abstraktionen realer Prozesse. In einer bestimmten Notation vorliegende Geschäftsprozesse können als visualisierte Worte einer formalen Sprache angesehen werden. Formale Fehler in der Modellierung lassen sich aus diesem Grund automatisch auffinden. Existieren darüber hinaus weitere Regelsysteme, die Simulationen ermöglichen, eine Generierung eines Workflow-Codes oder die Umwandlung in eine andere Notation, so wird ein Sprachtransfer auf eine andere Sprach- und Abstraktionsstufe vorgenommen und automatisch eine Applikation oder zumindest eine erste Applikationsinstanz entwickelt.

Zweckmäßig ist es darüber hinaus, den verschiedenen Nutzergruppen durch entsprechend unterschiedliche Sichten auf verschiedenen Sprachebenen gerecht zu werden. Hierzu sind Aggregationen, abstraktere Darstellungsebenen für Führungskräfte, oder zusätzliche Einblendungen für eher systemtechnische Fragestellungen sinnvoll.

Im Hinblick auf die eingangs dargestellte wahrgenommene Kritik an BPMN ist genauer hinzuschauen, warum diese Notation, die von technischer Seite aufgrund ihrer Leistungsstärke in Richtung Automatisierung viel Anklang findet, auf der fachlichen Ebene weniger Zuspruch erhält. Möglich ist, dass gar nicht die Notation Kritik verdient, sondern eher eine fehlende zusätzliche, vereinfachte Sicht für die Praktiker.

In jedem Fall bleibt aber festzuhalten, dass eine möglichst umfassende Verständigung vor allem durch einheitliche Festlegungen und Standards unterstützt werden könnte.

Asteroth, Alexander; Baier, Christel, Theoretische Informatik. Eine Einführung in die Berechenbarkeit, Komplexität und formale Sprachen mit 101 Beispielen, Pearson Studium, München, 1-12, 193 -424 (2002).

Deutscher Bundestag, Drucksache 17/11473. 17. Wahlperiode. Gesetzentwurf der Bundesregierung. Entwurf eines Gesetzes zur Förderung der elektronischen Verwaltung sowie zur Änderung weiterer Vorschriften. In: Bundesminsiterium des Innern (Hersg.) http://www.bmi.bund.de/SharedDocs/Downloads/DE/Gesetzestexte/Entwuerfe/ Entwurf_EGovG.pdf?__blob=publication File aufgerufen 30.12.2012 (2012).

Hofstadter, Douglas R., Gödel, Escher, Bach, ein Endloses Geflochtenes Band, Klett-Cotta, Stuttgart (1985).

Freund, Jakob; Rücker, Bernd, Praxishandbuch BPMN 2.0, Hanser, München, Wien (2009).

Rechenberg, Peter, Was ist Informatik. Eine allgemeinverständliche Einführung, Hanser, München, Wien, 180-185 u. 254-256 (2000).

 

---

 

Dagmar Lück-Schneider, Professorin für Verwaltungsinformatik, Hochschule für Wirtschaft und Recht Berlin, Fachbereich Allgemeine Verwaltung.

 

---