Jusletter IT

„Ich kenne im Augenblick kein Verfahren, das […], einmal erlernt, so leicht zu beherrschen ist, so übersichtlich und so wenig aufwendig ist.“ [ Cornides 1977, 272]

Die sog. Gegenformelmethode (Eng.: counter-formula method), fortan GFM, ist ein von R. Klinger und I. Tammelo am Ende der 1960er¹ an der Universität Sidney entwickeltes syntaktisches Verfahren (d.h. ein Kalkül) für Systeme der klassischen Aussagen- und Prädikatenlogik. Die Methode, die mit der Absicht konzipiert wurde, den praktischen Ansprüchen des Rechtsdenkens gerecht zu werden,² wurde im Laufe der 1970er insbesondere von H. Schreiner, G. Moens und I. Tebaldeschi – nebst Tammelo selbst – weiterentwickelt. Aus dieser Arbeit sind u.a. auch mehrere Varianten der GFM sowie neue Kalküle entstanden.³ Der vorliegende Beitrag diskutiert die GFM mit besonderem Fokus auf ihre Einordnung als syntaktisches Verfahren in der Logik (Abschnitt 3) sowie auf ihre Bedeutung in der Rechtswissenschaft (Abschnitt 4), dabei insbesondere in der Entwicklung der Rechtslogik und als Instrument der juristischen Methodenlehre. Erforderliche Vorkenntnisse werden im Abschnitt 2 in Grundzügen eingeführt. Abschnitt 3.3 liefert einen neuen Adäquatheitsbeweis für die GFM in Bezug auf die klassische Aussagenlogik.

Obgleich sowohl I. Tammelo als auch R. Klinger Logik ursprünglich in der heute allgemein gebräuchlichen, auf Peano/Russel bzw. Hilbert/Ackermann zurückgehenden Infixnotation gelernt haben [Tammelo 1974, 384], die Tammelo in seinen früheren Schriften noch bevorzugte [Tammelo 1955, Tammelo 1959], wird die GFM (ebenso wie die meisten rechtslogischen Abhandlungen der „Tammelo’schen Schule“) in der von J. Łukasiewicz entwickelten Präfixnotation (mitunter polnische oder Łukasiewicz-Notation) aufgebaut. Wie schon von der Bezeichnung nahegelegt besteht der Grundgedanke bei dieser Notation darin, dass Operatoren nicht wie in der Infixnotation zwischen ihren Argumenten, sondern vor ihnen gesetzt, d.h. nicht infixiert, sondern präfixiert werden. Diese Notation kann nicht nur mit logischen, sondern allgemein mit allen Arten von Operatoren, z.B. auch mit einfachen arithmetischen Operatoren verwendet werden. So kann man bspw. die Addition aus zwei und eins, die in Infixnotation als „2+1“ formuliert wird, in Präfixnotation durch „+21“ darstellen. Zur Veranschaulichung werden in der folgenden Tabelle mehrere Beispiele angeführt.

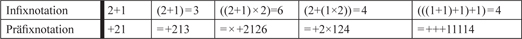
Tabelle 1: Infix- und Präfixnotation bei einfachen arithmetischen Ausdrücken

Der augenscheinlichste Vorteil der Łukasiewicz-Notation besteht darin, dass sie keine Klammern benötigt. Da die Anzahl von Argumenten jedes Operators festgelegt ist, lässt sich ohne Klammern stets eindeutig bestimmen, welche Argumente zu welchen Operatoren gehören. So können Berechnungen bzw. maschinelle Verarbeitungen von Formeln erheblich vereinfacht werden. Deswegen wird die Präfixnotation (und auch die invertierte polnische Notation, d.h. die Sufixnotation, die ebenso klammerfrei ist) in vielen Programmiersprachen und sonstigen Computeranwendungen (historisch vor allem Taschenrechnern) bevorzugt. Hinzu kommt der ehedem nicht unerhebliche Umstand, dass die logischen Operatoren in der Łukasiewicz-Notation nicht durch Pfeile und sonstige Sonderzeichen, sondern durch normale Großbuchstaben dargestellt werden, sodass sie ohne Schwierigkeiten mit einer üblichen Schreibmaschine getippt werden konnten.

Neben diesen Vorteilen wurde Klingers und Tammelos Entscheidung für die polnische Notation durch den Umstand motiviert, dass viele unter den führenden Namen in der damaligen Forschung zur Normen- und Rechtslogik ebenfalls die Präfixnotation verwendet haben.⁴

Die klassische zweiwertige Aussagenlogik (fortan AL) beschäftigt sich mit den einfachen logischen Beziehungen zwischen Aussagen, d.h. Ausdrücken, für die angenommen werden kann, dass sie entweder wahr oder falsch sind. Sie untersucht, welche Aussagen unter allen Umständen als wahr gelten müssen (sog. Tautologien) bzw. welche Schlussfolgerungen gezogen werden können, wenn angenommen wird, dass gewisse Aussagen wahr bzw. falsch sind. Ein System der AL kann wie folgt aufgebaut werden.

Zugrunde liegend ist ein vierelementiges Alphabet, d.h. eine Menge von Zeichen ℒ={φ, *, C, ‾}. Unter allen möglichen Zeichenreihen über diesem Alphabet wird die Menge WFF der (wohlformulierten) Ausdrücke (wff) der AL als die Menge aller Zeichenreihen definiert, die die Bedingung erfüllen:

1. Das Sternchen (*) wird nur als Index (in beliebiger Anzahl) für φ verwendet; Überstriche (¯) werden (in beliebiger Anzahl) nur auf φ bzw. C gesetzt.
2. Kommt das Zeichen C (mit beliebig vielen Überstrichen) n-Mal (n≥0) vor, so kommt das Zeichen φ (mit beliebig vielen Überstrichen bzw. Indexiert durch beliebig vielen Sternchen) n+1-Mal vor.
3. Wird die Anzahl der Vorkommnisse von C bzw. φ (mit beliebig vielen Sternchen bzw. Überstrichen) in einer (Teil-)Zeichenreihe durch |C| bzw. |φ| dargestellt, so gilt: Zählt man |C| bzw. |φ| von rechts nach links auf, so gilt zu jedem Schritt der Aufzählung |φ| |C|.

Intuitiv entspricht jedes mit n Sternchen indexiertes φ jeweils einer atomaren Aussage, etwa:

Tabelle 2: Beispiele für Aussagen

Wiederum ist C der Subjunktions- (d.h. Implikations-), der Überstrich (¯) der Negationsoperator.⁵ Cφ****φ** soll sodann den natursprachlichen Ausdruck abbilden: „Wenn es keinen Corona-Ausbruch in Salzburg im Februar 2023 gibt, dann findet das IRI§2023 in Salzburg statt.“ CφCφφ entspricht wiederum dem allgemeingültigen (tautologischen) Ausdruck „Wenn Jannik schöne Texte schreibt, dann gilt es: Wenn es nicht der Fall ist, dass Jannik schöne Texte schreibt, dann schreibt Jannik schöne Texte.“ Der Übersichtlichkeitshalber werden im Folgenden die Kleinbuchstaben p, q, r, … als Metavariablen für Aussagen verwendet.

Der Grad eines Ausdrucks wird wie folgt definiert: Ein jeder atomarer Ausdruck hat den Grad null. Hat p den Grad n, dann hat p den Grad n+1. Haben p und q die Grade m bzw. n, dann haben Kpq, Apq, Cpq und Epq den Grad m+n+1.

Die Semantik (Modelltheorie) von AL lässt sich relativ einfach aufbauen: Eine Funktion β auf WFF in die Menge {W, F} (für die Wahrheitswerte wahr bzw. falsch) heißt eine (Boole’sche) AL-Wahrheitsbelegung, wenn sie die Bedingungen erfüllt:

1. B(C): β(Cpq) = W genau dann, wenn β(p) = F oder β(q) = W.
2. B(¯): β(p) = W genau dann, wenn β(p) = F.

Ein Ausdruck p heißt eine Tautologie, wenn p unter allen möglichen AL-Wahrheitsbelegungen wahr ist. In diesem Fall schreibt man |=_AL p. Ein Ausdruck p heißt eine Dyslogie, wenn p unter keiner AL-Wahrheitsbelegungen wahr ist. In diesem gilt (wegen B(¯)) |=_AL p. Schließlich heißt ein Ausdruck eine Amphilogie, wenn er weder eine Tautologie noch eine Dyslogie ist.⁶

Die übrigen gewöhnlichen logischen Operatoren lassen sich wie folgt definieren:

Tabelle 3: Definition weiterer logischer Operatoren

Die GFM ist ein syntaktisches Verfahren. Das bedeutet im Allgemeinen, dass sie allein anhand syntaktischer Transformationen, d.h. grob formuliert allein durch das Operieren mit der äußerlichen Erscheinung von Zeichenreihen (im besten Falle) darauf zielt, zu bestimmen, zu welcher der oben durch semantische Überlegungen definierten Kategorien (Tautologie, Dyslogie, Amphilogie) ein jeweils gegebener AL-Ausdruck gehört.

Die GFM besteht aus einer Menge von Regeln, die die Ableitung neuer Ausdrücke aus einem gegebenen Ausdruck ermöglichen. Ziel der GFM ist es, durch die Anwendung dieser Regeln zwei sich widersprechende Ausdrücke abzuleiten. Die Beziehung zwischen solchen Ausdrücken wird Formel-Gegenformel (F-GF) genannt. Dabei gilt: Ist p eine Formel, dann ist p die entsprechende Gegenformel. Die Regeln der GFM werden in der folgenden Tabelle dargestellt:

Tabelle 4: Die Regeln der GFM

Hinzu kommt eine sog. Positionsumordnungsregel, die es erlaubt, die Glieder einer Disjunktion beliebig umzutauschen, solange dabei die Definition des wohlformulierten Ausdrucks beachtet wird. Der Übersichtlichkeit halber wurden auf der Tabelle die Regeln R1, R2, R5 und R6 lediglich in ihren einfachsten Sonderfällen dargestellt. Es ist wichtig, zu beachten, dass R1 und R2 auch auf einzelnen Teilausdrücke angewendet werden können. R5 und R6 sind wiederum allgemeine Regeln für die Reduktion bzw. Kontraktion von Disjunktionen. So kann z.B. aus AApqr und p durch R5 der Ausdruck Aqr gewonnen werden.

Ein Ausdruck p wird durch die GFM getestet, indem die Regeln der GFM auf p angewendet werden. Ein solcher Test ist abgeschlossen, wenn er erfolgreich ist oder spätestens, wenn keine Regel der GFM auf p oder auf einen aus p im Rahmen der Anwendung der GFM abgeleiteten Ausdruck q anwendbar ist. Ein Test heißt erfolgreich, wenn zwei Ausdrücke q und q abgeleitet werden, d.h. wenn eine Relation Formel-Gegenformel (F-GF) hergestellt wird. Ist ein Test durch die GFM für p erfolgreich, dann ist T ein Theorem der Gegenformelmethode. In diesem Fall schreibt man |–_GFM p.

Aufgrund ihrer Struktur kann die GFM als eine Form von Baumkalkül betrachtet werden. Insbesondere weist sie starke Ähnlichkeiten mit der Methode der analytischen Tableaux R. Smullyans (fortan ATS) auf.⁷ Allerdings mit der Besonderheit, dass der generierte Baum aus einem einzigen Ast besteht – um Lorenzens Ausdrucksweise zu benutzen, ist der Baum unverzweigt. Es ist daher angebracht, die GFM mit den ATS zu vergleichen.

Die Methode der ATS enthält zwei Regeltypen, nämlich A- und B-Regeln. Bei einer A-Regel werden zwei Ausdrücke α₁ und α₂ aus einem Ausdruck α im selben Ast abgeleitet. Bei einer B-Regeln entsteht wiederum eine Verzweigung: Zwei Ausdrücke β₁ und β₂ werden aus einem Ausdruck β jeweils in einem Ast abgeleitet. Dabei gilt:⁸

Tabelle 5: α- und β-Ausdrücke

Durch die Anwendung dieser Regeln auf einen AL-Ausdruck entsteht ein Baum mit einem oder mehreren Ästen. Ein Ast wird geschlossen, wenn in ihm sowohl ein Ausdruck p als auch ~ p in diesem Ast abgeleitet werden. Dies wird in diesem Ast mit einem „X“ gekennzeichnet. Ein Baum heißt geschlossen, wenn all seine Äste geschlossen sind; sonst ist der Baum offen. Ist der für einen Ausdruck ~ p erzeugte Baum geschlossen, dann ist p ein Theorem der ATS. In diesem Falle schriebt man |–_ATS p.

Zur besseren Veranschaulichung beider Methoden zeigt Tabelle 6 unten den Beweis einer aussagenlogischen Tautologie als Theorem sowohl der GFM als auch der ATS. Die jeweils angewendeten Regeln werden rechts von den abgeleiteten Ausdrücken in kursiver Schrift angegeben.

Sieht man vom Notationsunterschied ab, sind die zwei Beweise recht ähnlich. Der erste wesentliche Unterschied besteht darin, dass nur die GFM Umschreibungsregeln einsetzt, was den Beweis beträchtlich länger macht. Dies könnte umgangen werden, wenn man Kategorien von Regeln wie bei den ATS definieren würde. In der Tat lassen sich alle A-Regeln der ATS aus R1 bzw. aus Kombinationen von R3 mit den Umschreibungsregeln der GFM wiedergewinnen: Die erste bzw. die vierte Zeile der Tabelle 5 entspricht schon direkt der Regel R3 bzw. R1 der GFM; die zweite ergibt sich aus R3 mit AD; die dritte aus R3 mit CD. Auf diese Weise könnten im GFM-Beweis die Zeilen (1’), (2’), (6’) und (9’) unterdrückt werden.

Der zweite wesentliche Unterschied besteht wiederum darin, dass nur die ATS Regeln beinhalten, die zur Entstehung mehrerer Äste führen (B-Regeln). Dies passiert im ATS-Beweis auf der Zeile (6); hier sind die abgeleiteten Ausdrücke β₁ und β₂ jeweils ~((p→p)→p) bzw. ~ r. Letzterer führt zur sofortigen Schließung des entsprechenden Asts, da r bereits auf Zeile (4) abgeleitet wurde. Der Beweis wird sodann auf dem Ast mit ~ ((p→p)→p) fortgeführt. Beim GFM-Beweis war diese Verzweigung nicht nötig, weil R5 den direkten Übergang von ACCpppr und r auf CCppp (d.h. ~ ((p→p)→p)) ermöglicht hat (vgl. Zeile (5’)).

Die beim GFM-Beweis nicht verwendeten Regeln R2, R4 und R6 sind auch mit der Vermeidung von Verzweigungen verbunden: R2 vermeidet die Entstehung neuer Äste in einem trivialen Fall. R4 und R6 dienen der Vorbereitung für die Anwendung von R5.

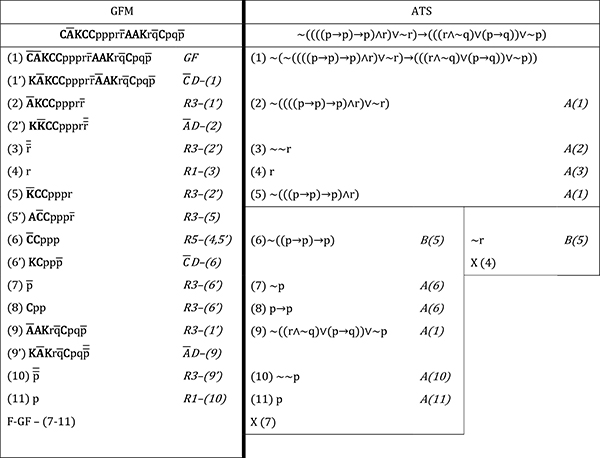
Tabelle 6: Beweis eines Theorems mit der GFM und mit den ATS

Selbst mehrere Jahre nach ihrer Konzeption wussten die Entwickler der GFM noch nicht mit Sicherheit, ob es sich dabei um ein adäquates Verfahren handelt oder nicht [Tammelo/Schreiner 1974, 12]. Ein erster Vollständigkeitsbeweis wurde bereits im Jahre 1974 skizziert und in [Lorenzen 1977] veröffentlicht (derselbe Beweis wird auch in [Inhetveen 1978] dargestellt). Bei diesem Beweis wird aufgrund der Umschreibungsregeln zunächst angenommen, dass alle Ausdrücke nur aus Konjunktionen und Disjunktionen zusammengesetzt werden können. Dies ist zwar formal korrekt, hat allerdings den Nachteil, dass dies nicht der üblichen Handhabung der GFM entspricht. Hier wird ein alternativer Beweis angeführt, der neben Lorenzens Ideen auch die strukturellen Ähnlichkeiten zwischen der GFM und den ATS zunutze macht. Die Argumentation basiert größtenteils auf Smullyans eigenem Adäquatheitsbeweis für die ATS [Smullyan 1995, 25ff.]. Um den Beweis zu vereinfachen, wird im Folgenden außerdem angenommen, dass die Regel R4 durch eine entsprechende Umschreibungsregel R4’: ApKqr ⇒ KApqApr ersetzt wird, woraus man mit R3 sofort R4 wiedergewinnt.

Zu zeigen ist, dass die GFM in Bezug auf die AL-Semantik adäquat ist, d.h. erstens: Wenn ein Ausdruck p ein Theorem der GFM, dann ist er eine Tautologie der AL; sowie zweitens: Wenn ein Ausdruck p eine Tautologie der AL ist, dann ist er ein Theorem der GFM, kurz:

1. Wenn |–_GFM p, dann |=_AL p (Korrektheit).

2. Wenn |=_AL p, dann |–_GFM p (Vollständigkeit).

Man nehme |–_GFM p an. Dann wird p erfolgreich durch die GFM getestet, d.h. die Anwendung der Regeln der GFM auf p führt zur Herstellung einer Relation F-GF (vgl. oben Abschnitt 3.1). Damit |=_AL p nicht gilt, muss es eine AL-Wahrheitsbelegung β geben, sodass β(p) = F bzw. β(p) = W. Sind nun q₍₁₎, q₍₂₎, … die Ausdrücke, die im Rahmen eines (evtl. nicht abgeschlossenen) GFM-Tests für einen Ausdruck p abgeleitet wurden, dann gilt: Wenn eine AL-Wahrheitsbelegung β, die all die in p vorkommenden atomaren Aussagen berücksichtigt, dem Ausdruck q₍₁₎ den Wert W zuweist, dann weist sie konsequent auch den Ausdrücken q₍₂₎, q₍₃₎, … den Wert W. Beweis: Angenommen β(q₍₁₎) = W. Der Ausdruck q₍₂₎ entsteht aus q₍₁₎ durch die Anwendung entweder einer Umschreibungs- oder einer Zerlegungsregeln. All diese Regeln haben die Form Γ ⇒ Δ, wobei Γ und Δ (meist einelementigen) Mengen von Ausdrücken sind. In allen Fällen gilt: Wenn β(Γ) = W, dann auch β(Δ) = W.⁹ Denn die Umschreibungsregeln entsprechen bekannten Tautologien bzw. Interdefinitionsmustern zwischen den Operatoren. Auch für die Zerlegungsregeln kann dies sehr leicht gezeigt werden. Haben z.B. bei Regel R5 die Ausdrücke Apq und p den Wert W, dann muss auch der Ausdruck q den Wert W haben; denn sonst könnte Apq wider Annahme nicht den Wert W haben. Per Induktion lässt sich sodann zeigen, dass alle Ausdrücke q₍₂₎, q₍₃₎, … den Wert W unter einer AL-Wahrheitsbelegung β annehmen, wenn β(q₍₁₎) = W. Gilt nun, wie oben angenommen, |–_GFM p, dann kann keine AL-Wahrheitsbelegung β allen q₍₂₎, q₍₃₎, … den Wert W zuweisen; denn die Anwendung der GFM auf p, d.h. q₍₁₎ hat zur Herstellung einer Relation F-GF unter den q₍₂₎, q₍₃₎, … geführt. Somit kann modo tollente q₍₁₎, d.h. p nicht den Wert W unter einer AL-Wahrheitsbelegung β annehmen. Daher muss, wenn |–_GFM p gilt, eine Dyslogie bzw. p eine Tautologie sein, d.h. es gilt |=_AL p.

Man nehme |=_AL p an. Damit |–_GFM p nicht gilt, muss der Test für p durch die GFM ohne Erfolg bleiben. Dass dies unmöglich ist, ergibt sich unmittelbar aus dem folgenden Hilfssatz:

Hilfssatz 1: Ist Σ = {q₍₁₎, q₍₂₎, …} die Menge aller Ausdrücke in einem abgeschlossenen, nicht erfolgreichen Test eines Ausdrucks p durch die GFM, dann sind alle Ausdrücke in Σ (inklusive p) gemeinsam erfüllbar, d.h. es gibt eine AL-Wahrheitsbelegung β, unter der alle Ausdrücke in Σ den Wahrheitswert W übernehmen.

Diese AL-Wahrheitsbelegung β würde also p den Wert W zuordnen, sodass wider Annahme |=_AL p nicht gelten kann. Hilfssatz 1 ergibt sich sofort aus den zwei folgenden Hilfssätzen.

Hilfssatz 2: Ist Σ = {q₍₁₎, q₍₂₎, …} die Menge aller Ausdrücke in einem abgeschlossenen, nicht erfolgreichen Test eines Ausdrucks p durch die GFM, so kann Σ auf eine sog. Hintikka-Menge Σ’ erweitert werden.

Hilfssatz 3 (Hintikka-Lemma): Ist M eine Hintikka-Menge, dann sind die Ausdrücke in M gemeinsam erfüllbar.

Mit diesen drei Hilfssätzen hat man: Wenn |–_GFM p nicht gilt, dann gilt auch |=_AL p nicht. Per Kontraposition erhält man den gesuchten Vollständigkeitssatz.

Beweis des Hilfssatzes 3: Eine Menge M von AL-Ausdrücken heißt eine Hintikka-Menge, wenn sie die folgenden Bedingungen erfüllt:

B1: Ist p ein atomarer Ausdruck, dann enthält M nicht sowohl p als auch p.

B2: Ist ein α-Ausdruck in M, dann sind auch α₁ und α₂ in M (vgl. oben Tabelle 5).

B3: Ist ein β-Ausdruck in M, dann ist β₁ oder β₂ in M.

Angenommen, M ist eine Hintikka-Menge. Eine AL-Wahrheitsbelegung β, so dass β(M) = W, kann wie folgt per Induktion nach dem Grad der Ausdrücke konstruiert werden: Ist p ein atomarer Ausdruck in M, dann setze man β(p) = W; ist wiederum p in M, dann setze man β(p) = F. Ist nun p ein Ausdruck n-ten Grades (n>1) und übernehmen alle Ausdrücke vom Grad n-1 in M unter β den Wert W, dann gilt: p ist entweder ein α-Ausdruck oder ein β-Ausdruck. Ist p ein α-Ausdruck, dann sind nach Annahme auch α₁ und α₂ in M; und weil α₁ und α₂ konsequent einen kleineren Grad haben als α, gilt bereits β(α₁)=W und β(α₂)=W. Damit gilt aber auch β(α) = W, d.h. β(p) = W. Ist p wiederum ein β-Ausdruck, dann ist nach Annahme entweder β₁ oder β₂ in M; und weil β₁ und β₂ konsequent einen kleineren Grad haben als β, gilt auch bereits β(β₁) = W oder β(β₂) = W, je nachdem welches von beiden in M enthalten ist. Dann ist aber auch β(β) = W, d.h. β(p) = W. Somit erhalten alle Ausdrücke in M durch β den Wert W, M ist also erfüllbar, was zu beweisen war.

Beweis des Hilfssatzes 2: Zu zeigen ist, dass Σ stets auf eine Hintikka-Menge erweitert werden kann. Weil Σ nach Annahme die Menge der Ausdrücke in einem nicht-erfolgreichen Test durch die GFM ist, erfüllt Σ bereits die erste Bedingung B1. Ferner können, wie bereits oben erwähnt, alle A-Regeln von ATS durch die Kombination von Regeln der GFM wiedergewonnen werden. Ist also ein α-Ausdruck in Σ, so sind auch die Ausdrücke α₁ und α₂ in Σ. Σ erfüllt somit auch B2. Demgegenüber ist B3 nicht immer erfüllt. Damit Σ zu einer Hintikka-Menge erweitert wird, muss Σ also durch diejenigen Ausdrücke β₁ oder β₂ ergänzt werden, die nicht abgeleitet wurden. Diese Ergänzung darf indes nicht zu einer Verletzung der anderen Bedingungen führen.

Wegen der Umschreibungsregeln und allenfalls der Positionsumordnungsregeln können alle β-Ausdrücke in Σ auf die Form |A|_n|z|_n+1 gebracht werden, wobei |A|_n eine Reihe von n≥1 Vorkommnissen von A und |z|_n+1 eine Reihe von n+1 Vorkommnissen von ggf. mit einem Überstrich markierten atomaren Ausdrücken r_j ist. Ist z einer dieser Ausdrücke, so ist es zwischen vier Fällen zu unterscheiden:

1. Die entsprechenden Ausdrücke β₁ oder β₂ sind bereits in Σ. Dies kann passieren, wenn sie aus einem α-Ausdruck abgeleitet wurden oder etwa dann, wenn R5 [Apq,p ⇒ q] auf z angewendet werden kann. In diesen Fällen ist die dritte Bedingung bzgl. z bereits erfüllt.
2. β₁ oder β₂ sind nicht in Σ, aber R6 [Apq, Apr ⇒ Aqr] (aber nicht R5!) kann auf z angewendet werden. Dann ist weder der jeweilige p noch p in Σ (sonst wäre R5 anwendbar). In diesem Fall ist Σ mit p oder p zu ergänzen und die einschlägigen GFM-Regeln sind anzuwenden. Mit R5 wird man die jeweiligen Ausdrücke β₁ oder β₂ für die entsprechenden β-Ausdrücke gewinnen können.
3. β₁ oder β₂ sind nicht in Σ und weder R5 noch R6 sind auf z anwendbar. Dann gibt es keinen Ausdruck q der Form |A|_n|z|_n+1 (mit n≥0) in Σ, so dass r_j in z und r_j in q ist (sonst wäre R5 oder R6 anwendbar). Dann ist Σ der letzte Ausdruck in der Reihe |z|_n+1 hinzuzufügen.

In den letzten zwei Fällen müssen die fehlenden Ausdrücke β₁ oder β₂ hinzugefügt werden, wodurch zwar B3 erfüllt wird, man allerding den Verdacht erheben könnte, dass dabei B1 verletzt werden könnte. Dass es nicht dazu kommt, lässt sich durch die folgenden Erwägungen zeigen: Sei u der erste auf die oben beschriebene Weise hinzugefügte Ausdruck. Damit die Hinzufügung von u zur Verletzung von B1 führt, muss es einen atomaren Ausdruck v geben, sodass aus der Ausdrucksmenge Σ∪{u} durch die GFM-Regeln v und abgeleitet werden können. Weil Σ die Menge der Ausdrücke eines abgeschlossenen, nicht erfolgreichen GFM-Tests ist, kann dies nur passieren, wenn entweder (1) einer der Ausdrücke v oder v bereits in Σ war und der andere aus Σ∪{u} abgeleitet wird; oder wenn (2) beide Ausdrücke v und v aus Σ∪{u} abgeleitet werden. Weil es stets nur um β-Ausdrücke geht (die Ableitungen mittels α-Ausdrücke ist durch die GFM bereits erledigt), kann dies nur durch die Anwendung von R5 geschehen. Dann muss im Fall (1) entweder Avu oder Avu und jeweils v oder bereits in Σ gewesen sein. In beiden Fällen müsste aber wegen R5 auch bereits in Σ sein, sodass die Hinzufügung von u nach dem oben beschriebenen Vorgang nicht zulässig (bzw. schon gar nicht nötig) wäre. Im Fall (2) müssten wiederum sowohl Avu als auch Avu in Σ sein, woraus man wegen R6 Auu und sodann wegen R2 u ableitet. Dann wäre wieder die Hinzufügung von u nicht zulässig.

Wie eingangs erwähnt wurde, betonen die Entwickler der GFM wiederholt, dass sie (insbesondere in ihrer prädikatenlogischen Fassung, wobei aber selbstverständlich kein Entscheidungsverfahren geliefert wird) ein für juristische Zwecke besonders geeignetes syntaktisches Verfahren darstellt. Tatsächlich werden mehrere Beispiele geliefert, wie die GFM für die Lösung von echten Rechtsfällen bzw. für die Prüfung juristischer Argumente angewendet werden könnte [Tammelo/Klinger 1974, 355ff.; Tammelo/Tebaldeschi 1976, 42ff.; Kolböck 1977; Tammelo 1978a, 106ff.; Schreiner 1981, 146ff.]. Dabei werden Fakten und Argumente zunächst in Natursprache beschrieben und sodann in logische Formeln übersetzt (mit der Anführung eines Glossars). Anschließend wird mit der GFM geprüft, ob die Annahmen widerspruchsfrei sind (sog. Gediegenheitsnachweis) bzw. ob die Konklusion aus den Prämissen folgt. Diese Prüfung könnte indessen nicht nur durch die GFM, sondern durch ein jedes adäquate syntaktische Verfahren erfolgen. Selbst Tammelo wendet andere Methoden, etwa die sog. Kurzweg-Tabularmethode auf Rechtsfälle an [Tammelo 1978a, 94ff.]. Warum sollte dann die GFM für das Rechtsdenken besonders geeignet sein? Ihre Entwickler scheinen drei Gründe zu nennen: (1) die klammerfreie polnische Notation, weil sie vor allem längere Ausdrücke erheblich vereinfacht [Tammelo 1974, 384], (2) die intuitive Übersichtlichkeit der GFM-Regeln [Tammelo 1978a, 55], (3) die Effizienz bzw. die Schnelligkeit der Beweisführung [Tammelo/Klinger 1974, 349], die nahezu maschinell erfolgt [Morscher 1978, 111; Schreiner 1984, 17f.]. Inwiefern diese Gründe überzeugend sind bzw. ob und inwiefern sie auch heute noch gelten dürften, ist fraglich: In Anbetracht der Möglichkeit, moderne, in digitalen Rechnern laufende SAT-Solver-Algorithmen für die Prüfung logischer Ausdrücke einzusetzen, scheinen die GFM und ihre Vorteile allenfalls nur wissenschaftshistorischen Wert zu haben.

Aber der Sinn der Rechtslogik geht weit über die je nach Standpunkt als utopische oder dystopische angesehene Bestrebung hinaus, Rechtsfälle durch symbolische Berechnungen zu lösen. Vielmehr dient sie dazu, die juristische Denk- und Argumentationsweise zu begreifen, zu verschärfen und sogar weiterzuentwickeln [Morscher 1978, 112f.]. Die Auseinandersetzung mit rechtslogischen Methoden – und die GFM ist eine aus dem Kern der rechtslogischen Praxis entstandene Methode – kann auch für die Grundlagenforschung in der Rechtsinformatik wegweisend sein. Man betrachte etwa die Form, wie Fälle durch die GFM gelöst werden: Die eigentliche Beweisführung hat nichts mehr mit juristischem Denken zu tun, sondern erfolgt rein maschinell. Nimmt man die Geltung der klassischen Logik für die juristische Argumentation an, so hängt die juristische Richtigkeit des Ganzen ausschließlich davon ab, ob und wie gut die Fakten und die Normen in logische Sprache übersetzt wurden. Dementsprechend haben sich auch Tammelo und andere Rechtslogiker intensiv mit den Herausforderungen bei der Formalisierung des Rechts auseinandergesetzt [Klinger 1971; Reisinger 1975; Tammelo 1978a, 71ff.]. Dem Prinzip nach ist das nicht anders, als wenn man versuchen würde, die Rechtsprechung zu automatisieren. Daher erscheint die Mutmaßung nicht unberechtigt, dass sich manche Lösungen für aktuelle und vielleicht sogar für zukünftige Forschungsfragen der Rechtsinformatik in den bereits erzielten Ergebnissen der Rechtslogik verstecken dürften.

Danksagung: Dieser Beitrag entstand im Rahmen des durch das BMWK geförderten Projekts „KI-Wissen – Automotive AI powered by Knowledge“. Der Autor bedankt sich beim Konsortium für die Zusammenarbeit.

Allen, Layman E., Symbolic Logic: A Razor-Edged Tool for Drafting and Interpreting Legal Documents, The Yale Law Journal, 1957, No. 6, S. 833–879.

Allen, Layman E., Propositional Calculi, MULL: Modern Uses of Logic in Law, 1959, No. 1, S. 4–14.

Anderson, Alan R., A Reduction of Deontic Logic to Alethic Modal Logic, Mind, 1958, No. 265, S. 100–103.

Beth, Evert, Formal Methods, D. Reidel, Dordrecht 1962.

Cornides, Thomas, [Rezension] Logische Verfahren der juristischen Begründung. Forschungen aus Staat und Recht, Bd. 35, by Ilmar Tammelo and Gabriel Moens, Archiv für Rechts- und Sozialphilosophie, 1977, No. 2, S. 271–273.

Hilbert, David/Ackermann, Wilhelm, Grundzüge der theoretischen Logik, Springer, Berlin 1928.

Inhetveen, Rüdiger, Die semantische Vollständigkeit der Gegenformelmethode. In: Tammelo, Ilmar/Schreiner, Helmut, Strukturierungen und Entscheidungen im Rechtsdenken. Springer, Wien 1978, S. 95–98.

Jeffrey, Richard, Formal Logic: Its Scope and Limits, McGraw-Hill Book Company, New York 1967.

Kalinowski, Georges, Théorie des Propositions Normatives, Studia Logica, 1953, I, S. 147–182.

Klinger, Ron, Die logische Struktur der normativ geschlossenen und der normativ offenen Rechtsordnungen, ARSP: Archiv für Rechts- und Sozialphilosophie, 1969, No. 3, 323–354.

Klinger, Ron, The Paradox of Counter-Conditional and its dissolution, Jurimetrics Journal, 1971, S. 189–193 (= University of Sydney Faculty of Law, Department of Jurisprudence and International Law (Institute for Advanced Studies in Jurispruidence) Materials for Postgraduate Studies, 1970, ALSP/IVR Special No. 2, 1970).

Kölbock, Karl, Logische Analyse eines wirklichen Rechtsfalles. In: Tammelo, Ilmar/Schreiner, Helmut, Grundzüge und Grundverfahren der Rechtslogik II, Verlag Dokumentation, München 1977.

Lemmon, Edward J., New Foundations for Lewis Modal Systems, Journal of Symb. Logic, 1957, No. 2, S. 176–186.

Lorenzen, Paul, Protologik. Ein Beitrag zum Begründungsproblem der Logik, Kant-Studien, 1955, 47, S. 350–358

Lorenzen, Paul, Die Vollständigkeit einer unverzweigten Variante des „analytischen“ Entscheidungsverfahrens der klassischen Logik“, Archiv für mathematische Logik und Grundlagenforschung, 1977, 18, S. 19–22.

Morscher, Edgar, Inwiefern betreffen Fragen der Vollständigkeit und Entscheidbarkeit den Juristen? In: Tammelo, Ilmar/Schreiner, Helmut (Hrsg.), Strukturierungen und Entscheidungen im Rechtsdenken, Springer, Wien 1978, S. 99–118.

Prior, Arthur N., Formal Logic, Clarendon Press, Oxford 1955.

Reisinger, Leo, Probleme der Symbolisierung und Formalisierung im Recht. In: Winkler, Günther (Hrsg.), Rechtstheorie und Rechtsinformatik, Springer, Wien 1975, 22–50.

Schreiner, Helmut, Die Eliminationsmethode als logisches Entscheidungsverfahren. In: Tammelo, Ilmar/Schreiner, Helmut (Hrsg.), Stukturierungen und Entscheidungen im Rechtsdenken, Springer, Wien 1978.

Schreiner, Helmut, Nuovi processi logici per ir ragionamento giuridico, Informatica e Diritto, 1979, Fascicolo n. 1, S. 115–137.

Schreiner, Helmut, Logische Redundanz als Instrument von Entscheidungsverfahren bei Rechtlichen Argumenten. In: Tammelo, Ilmar/Aarnio, Aulis (Hrsg.), Zum Fortschritt von Theorie und Technik in Recht und Ethik, Ducker & Humblot, Berlin 1981, S. 141–149.

Schreiner, Helmut, Ilmar Tammelos Leben und Werk. In: Krawietz, Werner/Mayer-Maly, Theo/Weinberger, Ota (Hrsg.), Objektivierung des Rechtsdenkens. Gedächtnisschrift für Ilmar Tammelo, D. & H., Berlin 1984, S. 5–18.

Smullyan, Raymond, First-order Logic, Dover, NewYork 1995.

Tammelo, Ilmar, Sketch for a Symbolic Juristic Logic, Journal of Legal Education, 1955, No. 3, S. 277–306.

Tammelo, Ilmar, On the Logical Structure of the Law Field, ARSP: Archiv für Rechts- und Sozialphilosophie, 1959, No. 1, S. 95–101.

Tammelo, Ilmar, Law, Logic and Human Communication, ARSP: Archiv für Rechts- und Sozialphilosophie, 1964, No. 3, S. 331–366.

Tammelo, Ilmar, Outline of Modern Legal Logic, Franz Steiner Verlag, Wiesbaden 1969.

Tammelo, Ilmar, 法論理学の原理と方法 [Principles and Methods of Legal Logic], 慶應義塾大学法学研究会 [Hogaku-Kenkyu-Kai Publication, Keio University], Tokio 1971.

Tammelo, Ilmar, On the Construction of a Legal Logic in Retrospect and in Prospect, ARSP: Archiv für Rechts- und Sozialphilosophie, 1974, No. 3, S. 377–392.

Tammelo, Ilmar, Modern Logic in the Service of Law, Springer, Wien 1978a.

Tammelo, Ilmar, Erneuerungsvorschläge für die logische Terminologie und Notation. In: Tammelo, Ilmar/Schreiner, Helmut (Hrsg.), Strukturierungen und Entscheidungen im Rechtsdenken, Springer, Wien 1978b, S. 53–63.

Tammelo, Ilmar/Klinger, Ron, The counter-formula method and ist applications in legal logic. In: Fischer, Michael/Jakob, Raimund/Mock, Erhard/Schreiner, Helmut (Hrsg.), Dimensionen des Rechts. Gedächtnisschrift für René Marcic, Ducker & Humblot, Berlin 1974, S. 349–360

Tammelo, Ilmar/Moens, Gabriël, Logische Verfahren der juristischen Begründung, Springer, Wien 1976.

Tammelo, Ilmar/Schreiner, Helmut, Grundzüge und Grundverfahren der Rechtslogik I, Verlag Dokumentation, München 1974.

Tammelo, Ilmar/Schreiner, Helmut, Grundzüge und Grundverfahren der Rechtslogik II, Verlag Dokumentation, München 1977.

Tammelo, Ilmar/Tebaldeschi, Ivanhoe, Il metodo della controformula e la sua applicabilità logico-giuridica. In: ders. (Hrsg.), Studi di Logica Giuridica, Dott. A. Giuffrè, Milano 1976, S. 25–49.