1.
Fragestellung ^
2.1.
Die «is-a»-Beziehung ^
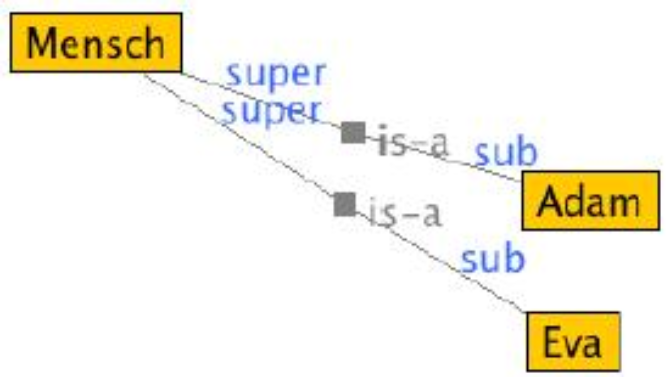
Diese Beziehung lässt sich einfacher als die anderen definieren. Sie entsteht zwischen einem abstrakten Begriff und den ihm zugeordneten konkreten Gegenständen. Beispielsweise gibt es zwischen dem Begriff «Mensch» (M) und dem Gegenstand «Adam» (m1) eine «is-a»-Beziehung, weil Adam ein Mensch ist. Man kann diese Beziehung auch als folgende Menge beschreiben:
M (m1, m2, m3...)
2.2.
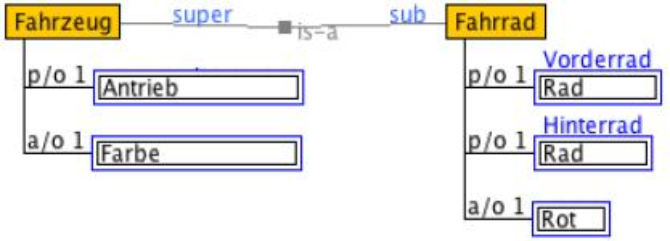
Die «part-of»-Beziehung ^
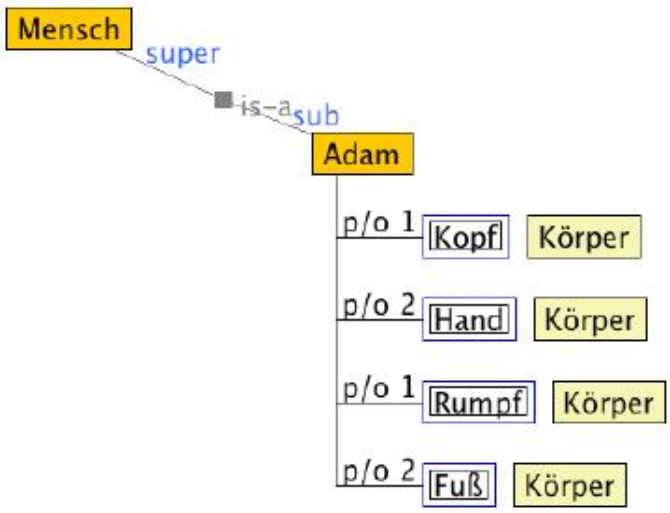
Meines Erachtens sollte man die «part-of»-Beziehung durch die is-a-Beziehung definieren. Das heißt, man kann sie formulieren, indem man die Elemente der is-a-Beziehung umordnet. Hier möchte ich ein Beispiel anführen. Vorausgesetzt, dass in der Welt nur Adam (m1) und Eva (m2) leben, dann lässt sich ohne Zweifel sagen, dass der Kopf von Adam ein Teil von ihm und der Kopf von Eva ein Teil von ihr ist («part-of»). Diese Erklärung gilt ebenso für ihre Hände, Füße und Rümpfe. Deshalb kann man Adam (m1) und Eva (m2) auf die folgende Weise als zwei voneinander getrennte Mengen beschreiben:
m1 (k1, h1, f1, r1)
m2 (k2, h2, f2, r2)
M (m1, m2) = M ((k1, h1, f1, r1), (k2, h2, f2, r2))
Aus dieser Formulierung folgt, dass zwar die Menge (k1, h1, f1, r1) Teile eines Menschen bedeutet, d.h., Adam ist ein Mensch, aber k1 ist kein Mensch. Denn niemand kann sagen, dass der Kopf von Adam ein Mensch ist. Diese Erklärung gilt auch für h1, f1, r1 und ebenso für die Teile von Eva (k2, h2, f2, r2). Daraus folgt als erste Regel:
- Regel 1: Wenn eine Menge etwas als Element enthält, bedeutet dies nicht immer, dass das Element ein dieser Menge zugeordneter konkreter Gegenstand («is-a») ist.
K (k1, k2)
M ((k1, k2), (h1, h2), (f1, f2), (r1, r2)) = M (K, H, F, R)
- Regel 2: Ein abstrakter Begriff kann nur abstrakte Begriffe als Teile haben.