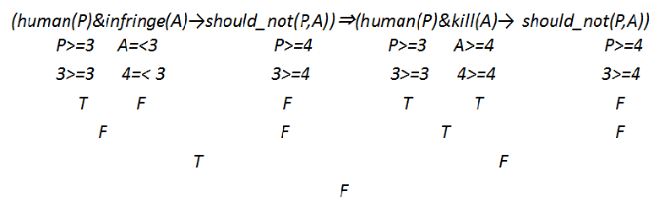Jusletter IT

Justice and Logic

The Role of Deductive Methods in the Reasoning of Justice

  • Author: Hajime Yoshino
  • Category: Articles
  • Region: Japan
  • Field of law: Legal Informatics, Artificial Intelligence & Law
  • Citation: Hajime Yoshino, Justice and Logic, in: Jusletter IT 11 September 2014
This paper aims to clarify the role of logical deductive methods in the reasoning of justice. Many traditional legal theories endeavored to present a deductive system of legal norms where concrete legal norms are deduced from abstract general norms or principles. We analyze these theories, for example in the natural law theory of Samuel Pufendorf, logically to clarify that they seem to be deductive at the first glance but are not deductive in the precise logical sense. We make it clear that they are based not only on the reasoning of deductive justification but also on the reasoning of legal creation or discovery. We clarify the reasoning of creation of norms as a combination of the generation of hypothetical norms and the examination of concrete norms. We demonstrate that the former reasoning is to be formalized as an inductive reasoning and the latter reasoning is to be formalized as the reasoning of falsification in the sense of Karl Popper. On the way to analyze theories of justice, this paper clarifies that the concept of justice is to be interpreted as the concept of truth in logic.

Table of contents

  • 1. Introduction
  • 2. The applicability of classical logic to the reasoning of justice
  • 3. The placement of the concept of justice in logic
  • 4. On Samuel Pufendorf’s systematization of just legal norms
  • 5. The role of the deductive methods in the reasoning of justice
  • 6. Conclusion – Future tasks
  • 7. Acknowledgement

1.

Introduction ^

[1]
This paper aims to clarify the role of logical deductive methods in the reasoning of justice. The reasoning of justice is conceived here as a reasoning to provide criteria of justice which evaluate human behavior as just or unjust on an extensional way (i.e., a way of enumerating a set of just norms to evaluate human acts as just or unjust).
[2]
Many traditional legal theories have endeavored to present a deductive system of (just) legal norms where concrete (just) legal norms are deduced from abstract general (just) norms or principles, as was the case in modern natural law theories as well as in conceptual jurisprudences (Begriffsjurisprudenz). In this paper, we analyze these theories. For example, we review the natural law theory of Samuel Pufendorf, to clarify whether the systematizations are based on the deductive method. To describe the conclusion in advance, they seem to be deductive at the first glance but are not deductive in a precise logical sense and, therefore, they are considered quasi-deductive theories.
[3]
First, we discuss logical methods which are to be applied to the reasoning of justice. As the method of logic as a tool to analyze the reasoning of justice, we insist on applying classical mathematical logic directly and we exclude the application of the special logic for norms.1
[4]
Secondly, we discuss the placement of the concept of justice in logic and we present our position that the concept of justice is to be conceived as a truth concept.
[5]
Thirdly, we show that there are fundamentally two ways to approach justice (e.g., intensional and extensional descriptions of justice). We then concentrate ourselves on a discussion of the extensional way.
[6]
Fourth, we take up Pufendorf’s natural law theory as a representative example of the traditional legal philosophy which seems to deductively systematize norms as well as values of justice and discuss them critically in terms of genuine logical deductive methods.
[7]
Finally, we analyze the reasoning of justice on two dimensions, the reasoning to generate hypothetical just norms and the reasoning to test the hypothesis. We clarify the role of the deductive method in the reasoning of generation of hypothetical just norms as a scheme for induction. We clarify the role of the deductive method in the reasoning to test the hypothetical just norms as the hypothetico-deductive method by applying Karl Popper’s conception.
[8]
We close this paper with suggestions for how this line of work will be furthered.

2.

The applicability of classical logic to the reasoning of justice ^

[9]

As regards to the method of logic as a tool to analyze the reasoning of justice, we apply classical mathematical logic directly to the analysis of justice. In contrast, we do not apply a special logic of norms (e.g., deontic Logic).

[10]
There has not been a special logic of norms developed which is reliable to be applied to real legal problems. It would be a time consuming and dangerous enterprise for us legal philosophers to develop a special logic of norms for ourselves.
[11]
According to our opinion, the devices of classical mathematical logic (e.g., predicate logic in first order) can be applied to norms without any essential difficulty. However, some restrictions and extensions of devices of predicate logic would be desirable2.
[12]

The scholars who refrain from applying classical logic to legal norms stress the semantic nature of norms as their reason. Such a viewpoint is based on the following two assumptions and the inference resulting from them («Dilemma of J¢rgensen»)

  1. Norm-sentences cannot be described as true or false.
  2. The system of classical logic is based on the evaluation of sentences in respect of true or false.
  3. Classical logic, therefore, cannot be applied to norm-sentences.
[13]
The inference from 1 and 2 to get 3 is questionable because the use of the term «true» in assumption 1 and 2 is not identical.
[14]

The pessimistic view in regard to the applicability of classical logic to norm-sentences results from a misunderstanding of the concept of truth in logic which is not identical with the normal epistemological truth-concept. Therefore, it is important to first review the truth-concept of logic before further discussion.3

[15]
The truth-valuation (i.e., the assignment of truth-values, for an atomic proposition-formula in predicate logic) can be defined as described in (A) and (B) below according to Tarski’s formal semantics if the following symbols are used:

Φ: a single-term predicate

i: an interpretation-functor

α1, ... , αn: individual constant or variable

(A) Φ(α1, ... , αn) is true under i if

(B) Φ(α1, ... , αn) is false under i if

[16]
Accordingly, when an interpreted individual constant or variable is an element of the set which is the extension of the interpreted predicate, then the relevant proposition-formula is true and, if not, then it is false. For a better understanding of this principle, a visual illustration will be given with a one-term predicate in Figure 1:

[Figure 1]

[17]
Based on the foregoing demonstrations, one should point out that the definition by Tarski of the truth-concept of logic is constructed purely formally. It is not questioned by what criteria the fulfillment must be decided. For the concept of truth in logic, the criteria which determine the fulfillment relations discussed above do not matter. The truth-valuation of statements in logic does not require that the fulfillment relations in question are «determinable through observation»4.
[18]
Logical calculations merely need the presupposition of the above relations (i.e., either the affirmation or negation of the element relationship of a set) from any standpoint. Under such a presupposition, the kind of fulfillment relations is to be calculated by logic. According to the definition by Tarski, the logical calculus needs, as a presupposition, nothing but the purely formal principle of bivalence, namely, that a value of two possible values is allocated to every sentence uniformly5.
[19]
Legal sentences can be evaluated as valid or invalid using certain criteria. Such a bivalent evaluation can be made to every legal sentence. Therefore, the concept of truth in logic is applicable to legal sentences. As a conclusion, classical logic can be applied to the normative world of discourse.

3.

The placement of the concept of justice in logic ^

[20]
What is the placement of the concept of justice in logic? In other words, how is the concept of justice to be treated in the devices of logic? In our opinion, the concept of justice is to be treated as the truth concept in logic. We would like to explain the reason of this conception at first and then discuss the way we represent the concept of justice on the basis of this conception.
[21]
The structure of justice-judgment can be compared to one of fact-judgment, which can be made apparent using the following example:

(a) It is just that all humans must be punished if they have killed another human.

(b) It is unjust that all humans must be praised if they have killed another human.

(a’) It is true that all iron expands if it is heated.

(b’) It is false that all iron contracts if it is heated.

[22]
From this comparison, the following can be induced. Both sentences have the same syntactic structure: «just» (or «unjust») in justice-judgment is located in the same place as «true» (or «false») in fact-judgment. Similar to the latter concept being treated as a truth concept in logic, one could understand that the former concept could be treated as a truth concept in logic as well. One could treat the concept of justice as the truth concept in logic. We would like to ground this interpretation by means of formal semantics.
[23]
In the previous chapter we discussed the definition of the truth concept presented by Tarski. This definition can be applied to the interpretation of the concept of justice as a truth value in logic.
[24]
If «Φ» is applied to an atomic predicate with n-terms and «α₁», … , «αn» to an individual constant and a variable, then the truth-valuation (i.e., the allocation of truth-values to an atomic proposition in predicate logic) is represented as follows:

(A’) Φ(α₁, … , αn) is just if and only if< i (α₁), … ,i (αn)>∈ i(Φ)

(B’) Φ(α₁, … , αn) is unjust if and only if< i (α₁), … ,i (αn)> ∉i(Φ)

[25]
When an individual constant or variable comes under a predicate (i.e., when an interpreted individual constant or variable falls under the class of the interpreted predicate), then the proposition is «just» (A’) and otherwise it is not «just», namely «unjust» (B’).
[26]
This relationship in the case of a proposition with a one-term predicate can be represented in the following Figure 2:

[Figure 2]

[27]
This definition of the concept of justice as a truth concept in the case of a single proposition introduced above can be extended to complex conditional sentences (i.e., rule sentences which have a general logical structure of legal norms) as in an example below:

(a’) It is just that all humans must be punished if they have killed another human.

(b’) It is unjust that all humans must be praised if they have killed another human.

[28]
In this norm, an individual constant or variable, which belongs to the class of «being an entity who has killed another human» in the antecedent, can come under the class of «must being punished» in (a’) in the consequent, but not under the class of «must being praised» in (b’). It is understandable that the state of affairs in (a’) is «just» and in (b’) is «unjust».
[29]
This example has been applied to the figures shown before in the following way (Figure 3):

[Figure 3]

[30]
As the meaning of words can be defined on an intensional and extensional way, the concept of justice can be defined intensionally and extensionally as well. The intensional definition of the concept of justice is to define the nature of justice. The extensional definition of the concept of justice is to define a set of just legal norms. The extension of justice as a truth concept is the set of legal norms which are evaluated as just. If the concept of justice is to be interpreted as the truth concept, the intensional description of justice is as difficult as the intensional description of the truth concept is difficult. On the contrary, it is easier to extensionally enumerate legal norms which are evaluated as just. To decide the set of just legal norms step by step, enumerating just norms is a productive way for us to approach the concept of justice. We would like to discuss away to decide a set of norms are just.

4.

On Samuel Pufendorf’s systematization of just legal norms ^

[31]
When speaking of the role of deductive methods, one may at first think of deductive system-building of just norms in modern natural law theories. Samuel Pufendorf developed the theory in which individual’s rights and duties are derived from the fundamental principle of natural law.6
[32]
He considered the nature of humans as «sociability» (N). From this nature, he sets a fundamental principle of natural law:
[33]
«Every Man … should cultivate and preserve toward others a sociable attitude, which is peaceful and agreeable at all times to the nature and end of human race.» (p)
[34]

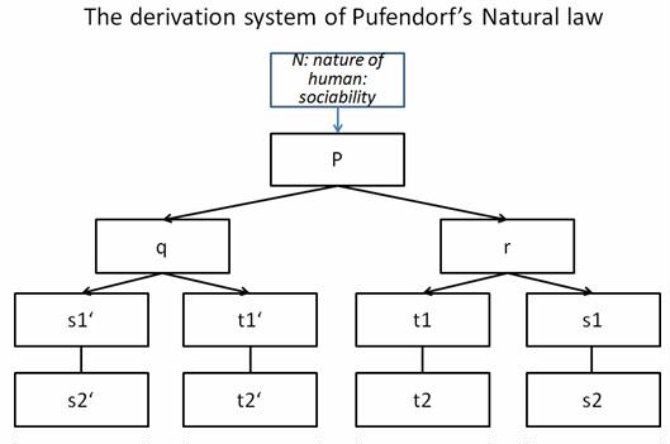
He thought that this supreme, most general natural law contains all particular natural laws and the latter can be deduced from the former and be reduced to it.7 Thus, starting from this extremely general and abstract fundamental natural law principle (p), he derived:

[35]

(1)The natural law norm of humans’ action for himself (q) and (2) the natural law norm of humans’ action for other persons (r).8 From this natural law norm (r), he derived «absolute norms» (s), obligating all men and «hypothetical norms», depending on human’s judgment (t). These are more particular and concrete norms of natural law.

[36]

As the derivation of (s) from (p) through (q), he derived: «I. No one should hurt another (s1’) and II. If he has caused another a loss, he should make it good (s2’).»9 As the derivation of (s) from (p) through (r), he derived the norm10: «If one has done another some hurt, (s1) … the aggressor must, as far as he can, make good the loss.» (s2)

[37]
As the derivation of (t) from (p) through (q), he derived the norm11: If one entered a contract (t1’), he is obliged to follow certain commands, which arise because of his entrance (t2’), e.g. to pay the money for the purchase goods. Similar duties are derived through (r) for the other party of the contract (t2) after he entered the contract (t1).
[38]
The systematization by Samuel Pufendorf is represented by the following Figure 4:

[Figure 4]

[39]
In Pufendorf’s natural law system, more concrete norms are derived from general more abstract norms. The derivation of concrete norms from a general abstract norm seems at first glance to be deductive. But after an exact logical analysis, it becomes apparent that this is not deductive in logical sense. We would like to test the logical correctness of the following example-model of such reasoning by the means of logic. For example, can the concrete norm «any person should not kill another human» be deduced from the general abstract norm «any person should not infringe the human personality»?
[40]
If the following example formulae are applied to the sentence:

«is a human»: human(p);

«infringe the human personality»: infringe(a);

«should not do a»: should_not(p,a);

«to kill human h»: kill(h), then the inference above is formalized as follows:

∀P∀A(human(P)&infringe(A)→should_not(P,A))⇒

∀P∀A(human(P)&kill(A)→should_not(P,A))

[41]

It can be proved that this inference formula is logically invalid because its antecedent is true and its consequence is false in the following interpreted case:

human(P):P>=3;

infringe(A): A=<3;

should_not(P,A): P>=A;

kill(A):A>=4.

This is the case when P=3 and A=4 as follows (Proof 1):(human(P) &infringe(A) ➙should_not(P,A))⇒(human(P)&kill(A) ➙should_not(P,A))

[Proof 1]

[42]
Therefore, this type of derivation is not a deductive inference.
[43]
Why do people conceive that such a derivation and systematization like Pufendorf’s is deductive? The reason is that people admit implicitly an additional presupposition, for example: «To kill another human is to infringe the human personality.»
[44]
If this is added to the original premise, the derivation becomes deductive. This is provable as follows (Proof 2):

[Proof 2]

[45]
According to the analysis above, we could conclude that this type of «deductive» reasoning is not a genuine deductive reasoning. In such «deductive» systematization, an additional premise, as implicit knowledge, is to be found or created and added.

5.

The role of the deductive methods in the reasoning of justice ^

[46]
We would like to at first discuss (1) types of the reasoning of justice and then analyze (2) the role of deductive methods in each type of the reasoning of justice.
[47]
We consider the reasoning of justice as a developing process of norm sentences. We analyze this process in two dimensions which are mutually related to each other: the reasoning of justification and the reasoning of creation or discovery. The reasoning of justification is the reasoning in which a justice judgment on a human act is justified as the logical consequence of the application of norm sentence already approved as just to the description of the act. The reasoning of creation is the reasoning where sentences which constitute the reasoning of justification are created or found. The «creation» of sentences here means that sentences are not deduced but newly set.
[48]
It is to be noted that concrete just norms cannot be deduced from abstract general principles as discussed above, but they can be explained or justified from the latter if one specifies the implicit knowledge mediating between the latter and the former. The mutual relation between the reasoning of creation and justification is represented in Figure 5:

[Figure 5]

[49]
Before the reasoning of justification is completed (i.e., the logical deduction process is completed), some of the sentences in this reasoning scheme are not justified (i.e., not deduced from norm sentences already approved as just). A justice judgment on a human act itself must be created at the beginning. The description of the human act must be created. The concrete just norm sentence which is the result of the concretization of the general abstract just norm to apply the latter to the description of the human act is to be created. The principle of justice which integrates various general just norms should be created in order that the system of just norms is constituted.
[50]
In the reasoning of justification, the deduction plays a decisive role. The logic guarantees the justness of a norm sentence when it is logically deduced from just norm sentences. The deduction is the ground of the justification. In the deduction, the inference rule Modus Ponens plays its role.
[51]
In the reasoning of creation of norm sentences, Modus Ponens plays a role as a framework in which new norms are to be created. On the systematization, the abstraction explained later plays its role as well.
[52]

The reasoning of creation or discovery is composed of two further types of reasoning which are mutually related to each other:

generation of hypothetical just norms and

testing the hypothetical just norms.

[53]
We think that the just norm is originally to be generated as a hypothesis. The generation is composed of two types of inductive reasoning: the goal-oriented induction and the abstraction-based induction.
[54]

The goal-oriented induction is the following:

goal: g(a),

fact: f(a)

generation: g(X)←f(X)

[55]
In order to prove goal g(a) on the basis of fact f(a), the rule g(X)←f(X) is to be generated. The deductive method Modus Ponens plays its role as a scheme here.
[56]

The abstraction-based induction is represented as follows:

concrete norms: g1(X)←f1(X), g2(X)←f2(X)

knowledge on concepts: g1⊂g, g2⊂g, f1⊂f, f2⊂f

abstraction: g(X)←f(X)

[57]
These two types of reasoning are to be performed related to each other.
[58]
In the reasoning of testing hypothetical norms generated, the logical deductive inference method, «Modus Tollens», plays a decisive role. Karl, R. Popper has proposed «the deductive method of testing» as the inference model of discovery in empirical sciences in his book The Logic of Scientific Discovery.12 According to Popper, theories are never empirically verifiable and not the verifiability but the falsifiability of a system is to be taken as criterion of demarcation.13
[59]
He described: «The falsifying mode of inference here referred to – the way in which the falsification of a conclusion entails the falsification of the system from which it is derived – is the ‹Modus Tollens› of classical logic.»14
[60]

We think that Poppers falsification model does fit to the method of testing hypothetical just norms. The inference to test a hypothetical norm is Modus Tollens, which is represented in propositional logic as follows:

(P→ Q) &￢Q⇒￢P

[61]
«P» represents a knowledge system with the hypothetical norm.
[62]

«Q» represents the consequence which follows from the system to which the new hypothesis is added. If Q is negatively evaluated (falsified: ￢Q), then the system including the hypothetical norm is to be negatively evaluated (falsified: ￢P) as well.We would like to represent this inference scheme more precisely identifying the system of the already existing knowledge and the added hypothesis as follows. If «R» is the whole of the existing knowledge, «r» is a new hypothetical norm, «E» is an event to which the hypothesis is applied and «C» is the consequence of the application of the whole existing knowledge together with the hypothesis, then the inference scheme of the falsification of the added hypothesis is:

｛（R ∪ r1）& E → C｝&￢C ⇒￢r1

[63]
The reasoning of justice should perform the simulation of falsification as much as possible so that a hypothetical norm which will bring no serious unjust result is found. The whole inference scheme of the falsification which leads to a «just» norm which is confirmed as not falsified is represented as in Scheme 1.

[Scheme 1]

[64]
The norm ri is to be confirmed as relatively just in the sense that it is not proved as unjust.
[65]
It is to be noted that the falsification model of the reasoning of justice fits the reality of legal practice in the following points:
  1. The creative evaluation of a legal sentence in legal practice is done mostly not on the positive way to evaluate it as just but on the negative way to evaluate it as unjust. The reason is that it is difficult to verify that a legal sentence is just but easier to falsify that it is unjust15.
  2. It may also be the reason that law must provide a certain norm to solve social disputes and to maintain an order in a society so that legal norms provided should be treated as temporally just unless they are proved to be unjust.
[66]
The evaluation of a legal sentence can be done more convincingly not on an abstract level of language but on a concrete level of language. One can evaluate it with more confidence on a concrete level than on an abstract level even if it is still subjective.
[67]
One should make his attention to that the judgment of justice as a value cannot be done objectively like in natural sciences but mainly subjectively. One should also notice that the inference to the result of the application of the knowledge in law cannot be done as precise as in natural sciences. From these reasons, it is to be noted that a single negative evaluation for a single case is, unlike in natural sciences, not enough to be succeeded in the falsification. One should reach a certain amount of negative evaluations of results of the application of the hypothesis.
[68]
The debates between persons who have different hypotheses and their evaluations play a particularly important role to achieve more just norms. In order to reach a decision through such a debate, one would need a procedure like a court or a parliament. In any case, the majority decision could be one of the methods in such procedures to reach a decision.

6.

Conclusion – Future tasks ^

[69]
We would like to conclude this paper with suggesting our further tasks in the theory of reasoning of justice.
[70]
As the logical structure of the reasoning of justice is more or less clarified, we should discuss how to develop an inference system of the reasoning of justice.
[71]
Although the concept of the truth itself is difficult to be defined in an intensional way, this does not nullify the value of analyzing the conditions of just or unjust norms. It is one of our further tasks to discuss how to describe these conditions, particularly, necessary conditions for legal norms to be determined unjust. As the law expresses the concept of the truth in the legal world by means of the predicate «valid» or «invalid» and settles legal meta-rules which regulate conditions for legal norms to be valid or invalid, we may try to find meta-rules which regulate conditions for legal norms to be just or unjust using the predicate «just» or «unjust».
[72]
We should discuss the way how to predict transparently and precisely the results of the application of (hypothetical) norms to possible events in the falsification reasoning of justice.
[73]
We think that the systematization of law as in Pufendorf’s system of natural laws may have been made, in fact, not top-down but bottom-up. This can be made visible with the help of the following Figure 6.

[Figure 6]

[74]
How can such a systematization be made? This process is to be analyzed from the logical point of view. In the near future, we will try to give our answer to this question in terms of Logical Jurisprudence, applying the study results of this paper.

7.

Acknowledgement ^

[75]

Prof. Friedrich Lachmayer is one of my best friends since 1974. He has always kindly supported my study of Logical Jurisprudence. I thank Friedrich very much for his support. With many thanks I would like to dedicate this paper to Friedrich. Prof. Erich Schweighofer has kindly invited me to contribute to these proceedings and patiently encouraged me to complete my paper. I thank Erich a lot for his warm encouragements. This paper is completed during my stay in Kiel as a visiting professor of the «Lehrstuhl für Öffentliches Recht und Rechtsphilosphie der Christian-Albrechts-Universität zu Kiel (Prof. Robert Alexy)». I appreciate Robert’s warmest support. My student-assistants in Kiel Regina Kardel, Dennis Hardtke and Sven Petersen have assisted me well, whom I am grateful to. This paper was checked by Prof. Jackson Wilson. I appreciate Jackson’s review.

 

Hajime Yoshino, Meiji Gakuin University.

Some of the original ideas of this paper were presented in my Japanese paper «Seigi to Ronri – Seigi-Suiron niokeru Enekiteki Hoho no Yakuwari» (Justice and Logic – The role of deductive methods in the reasoning of justice), in: Justice – Annual Report of Legal Philosophy 1974, Yuhikau Publishing Tokyo, 38-68. In the meantime, I developed the theory of legal reasoning through the studies on the artificial intelligence of law. This paper has much expanded from the previous paper by including various results of study on the theory of legal reasoning. On May 24th, 2012 at University of Lisbon, I gave a lecture titled «Justice and Logic – the role of deductive methods in the reasoning of justice» at the Third International Conference on Quantitative Justice and Fairness 2012, organized by Prof. Paulo Mendes at University of Lisbon and Dr. Rainhard Bengez at Technical University Munich . This paper has been written on the basis of my power point presentation submitted to the conference.

  1. 1 Cf. Yoshino, Hajime, «Über die Notwendigkeit einer besonderen Normenlogik als Methode der juristischen Logik», in: Klug, U. et. al. (Hrsg.), Gesetzgebungstheorie, Juristische Logik, Zivil- und Prozessrecht, Berlin – Heidelberg – New York, Springer Verlag, 1978, 140 ff. Below, this is abbreviated as Yoshino, 1978a.
  2. 2 Some restrictions are desirable for us in order to realize computational efficiency of legal reasoning, for example to restrict predicate logic into horn-clause logic as its subset and presuppose the closed world assumption. Some extensions are desirable for us to represent legal relations as entities using identifiers and case lists of legal terms. See: Yoshino, Hajime, «On the Logical Foundation of Compound Predicate Formulae for Legal Knowledge Representation,» in: Artificial Intelligence and Law, Vol. 5, No. 1, 77–96; Yoshino, H. and Sakurai, S., «Identification of Implicit Legal Requirements with Legal Abstract Knowledge,» in: Proc. The Fourth International Conference on Artificial Intelligence and Law, ACM (The Association for Computing Machinery), 1993, 298 f.
  3. 3 This is necessary also to understand the starting point of Logical Jurisprudence, because the truth concept is one of three primitives of Logical Jurisprudence.
  4. 4 Weinberger, Ota, Bemerkungen zu J. Rödig’s «Kritik des normlogischen Schließens», in: Theory and Decision 3 (1973), 314.
  5. 5 Cf. Yoshino, 1978a, 145.
  6. 6 Pufendorf Samuel, De Jure Naturae et gentium libri octo, Amsterdam Aufl. 1688, 143 ff. The translation by Oldfather, 208 ff.
  7. 7 Cf. Pufendorf, S., Eris scandica, 1686, 231 f.; Denser, Horst, Moralphilosophie und Naturrecht bei Samuel Pufendorf, München 1972, 289; Welzel, H., Naturrechtslehre Samuel Pufendorfs, Berlin 1958, 51.
  8. 8 Pufendorf, S., De Jure Naturae et gentium libri octo, Amsterdam Aufl. 1688, 143 ff. The translation by Oldfather, 229, 313 f.
  9. 9 Pufendorf, S., ibid., (3I.1) 213; cf. Translation, 313.
  10. 10 Pufendorf, S., ibid., 314.
  11. 11 Pufendorf, S., ibid., 229 f.
  12. 12 Popper, K., The Logic of Scientific Discovery, Hutchinson of London, 1959, 30.
  13. 13 Popper, K., ibid., 40.
  14. 14 Popper, The Logic of Scientific Discovery, Hutchinson of London, 1959, 46.
  15. 15 Cf. Edmond Cahn, The Sense of Injustice. New York 1949, 11–27.