Jusletter IT

Analogical Reasoning is central to legal reasoning in at least two of the major categories of legal systems: the codified law systems and the case law systems. In the former, analogical reasoning features at least in law development (Rechtsfortbildung), in the latter in the method of distinguishing. Arguably, however, already questions of mere interpretation and simple subsumtions of concrete facts under abstract legal norms require ampliative analogical reasoning: no legal agent – human or machine – can know enough subsumption rules to account for the infinite forms the facts of a case can take.¹

In spite of this, recent approaches in modelling legal reasoning have largely moved away from analogical approaches to rule-based ones². Such approaches have proven to be powerful in capturing the defeasible aspects of the law. However, while it is important to handle defeasibility it is crucial to remember that defeasibility is only necessary as a consequence of inconsistency which is in turn caused by unsound inference.

Humans pay the price of unsoundness to reap a reward: the ability to make ampliative inferences. Contrary to this, present rule-based systems do not offer a corresponding benefit by e.g. providing a mechanism that adds novel rules to their knowledge base. They remain analytic in the Kantian sense: any true proposition is already contained in the (skeptical, credulous) closure of their assumptions under the (strict and defeasible) components of their inference system filtered by an appropriate semantic (complete, grounded, ideal, preferred, …).

In a recent Festschrift for Erich Schweighofer, Trevor Bench-Capon tongue-in-cheek assures the former (and himself) of his job security as a Good-Old-Fashioned-AI-and-Law (“GOFAIL”) researcher by faulting machine learning for being inapplicable to case law due to its retrospectiveness (among other things: “When deciding a case, we are not discovering something common to the previous cases, we are creating a rule to decide a particular case, and which is intended to constrain future cases”³. In fairness it should be said that none of the current symbolic GOFAIL methods provide a mechanism to create rules either. In this paper we sketch a path towards such ampliative symbolic AI methods.

We begin by reviewing the literature on analogical reasoning. We then proceed by introducing context graphs in the OMDoc/MMT framework. We then provide a sketch of an ampliative inference algorithm operating on context graphs and go through an example in some detail. We conclude by outlining the path ahead towards the implementation of the algorithm sketch.

We can broadly categorize approaches to analogical reasoning⁴ along two dimensions: ampliativeness and normativity. Ampliative accounts of analogy count it among the inference modes that allow the generation of “new” knowledge such as induction or abduction. Non-ampliative accounts view analogies as enthymemic (i.e., “gappy”) deductive inference. Such enthymemes can be harmless, e.g., the result of omitting trivial minutiae as is often done in technical language among experts; or the enthymeme can be substantial, that is the argument cannot easily be completed, even by an expert. In the latter case non-ampliative analogy rests on the implicit assumption that such a deductive completion is possible. Normative accounts seek to establish reasoning schemes for ideal analogical argument; non-normative (descriptive) accounts aim at discovering the cognitive mechanism behind analogical reasoning.

The most important ampliative and normative theory is the structure mapping theory (SMT) of analogy.⁵ It has been implemented in the structure mapping engine (SME) algorithm.⁶ SMT judges two domains to be in analogy with each other if an embedding exists between them. The closer to isomorphism (in terms of the theory), the more systematic the embedding, the better the analogy. In the extreme case of an isomorphism the inference becomes deductive. Here the analogy is not seen in the formal structure but rather in shared factual observable properties.⁷ Finally Bartha’s articulation model⁸ focusses on theory construction: the similarities between the source and the target domain must be shown to be critical features of the source and not merely irrelevant ones. Likewise, no critical feature of the target domain may contradict a critical feature of the source domain.

Non-ampliative normative accounts date back to Aristotle’s argument scheme from his Rhetoric⁹. In modern times such an approach has been defended by Daves and Russel¹⁰ and Schlimm¹¹ in his axiomatic account. In these accounts the analogs are instances of an implicit (set of) axiom(s) yielding enthymemic arguments. Notably, the isomorphic special case of structure mapping implies this condition.

However, as Schlimm¹² points out, the inverse does not hold: two domains may obey the same axioms but no isomorphism between them may exist (e.g., the 2-group and the 3-group). Instead, the analogy is established by showing that both analogs obey the same axioms (in the example, the group axioms) or are instances (homomorphic images) of a more complex domain (in the example, the free group). As far as we are aware there are presently no implementations of Schlimm’s axiomatic account of analogy.

Finally, descriptive theories¹³ attempt to develop cognitively plausible mechanisms for analogical reasoning. They are usually based on connectionist models mimicking human neural processes. Connectionist models may also be highly useful as computational models for the normative theories. Implementations of connectionist models include ACME (Analogical Constraint Mapping Engine)¹⁴, LISA¹⁵ and Copycat¹⁶. Sowa and Majmudar’s¹⁷ VivoMind Analogical Engine claims to straddle SMT and connectionist approaches by implementing SMT “from the bottom up” on conceptual graphs using low-level label and subgraph matchings as well as subgraph transformations to discover high-level structure mappings.

In the legal domain, analogical reasoning has primarily been captured using a version of SMT. The similarity of cases is assessed based on aspects. That is, dimensions of cases that range from maximally pro-defendant to maximally pro-plaintiff and Boolean factors that pertain either to the defendant or to the plaintiff. Conflicting arguments for different possible precedent applications are then constructed based on the degree to which cases resemble each other in terms of their aspects.¹⁸ The main implementations of the analogical approach are the HYPO¹⁹ and CATO systems²⁰.

In the rule-based approach, precedents are taken to extend the existing body of law by their respective “rule of the case” which is encoded as a defeasible inference rule in the object language of some logic.²¹ Defeasibility is established through attacks (undercuts, rebuttals) and preference ordering over rules.

The most important systems include ASPIC+²² and abstract dialectical frameworks (ADFs) in conjunction with the ANGELIC methodology²³ which allows to encode factor hierarchies as ADFs which can in turn be implemented in a target language such as logic programming.

A (superficially) different approach is taken by the Carneades system.²⁴ Here links between premises and conclusion instantiate deductive or defeasible argument schemes. For validation, arguments are checked against the catalogue of available schemes.

Rule-based approaches allow to systematically treat the burden of proof and different proof standards through the use of default reasoning and prioritisation of rules respectively. However, Stevens²⁵ argues that the analogy-account for legal reasoning is preferable as it better accounts for judicial discretion and as a heuristic to find applicable precedents as well as reasons to distinguish a case – especially for novel cases. Aktionson and Bench-Capon²⁶ lament a lack of computational models for analogical reasoning.

We have already taken a step towards such a model (see Rapp et al. (2020)²⁷. There we combined rule-based and analogical reasoning to represent analogical reasoning and operationalize the critical questions for analogies established by Stevens. Here we focus on the algorithmic aspects of such reasoning and how it interplays with analytic deductive and argumentative reasoning.

OMDoc²⁸ is a wide-coverage representation language for mathematical knowledge (formal) and documents (informal/narrative). In the last decade development has focused on the formal aspect leading to the OMDoc/MMT instance (Meta-Meta-Theories^{29 30}), which increases expressivity, clarifies the representational primitives and formally defines the semantics of this fragment.

OMDoc/MMT is designed to be foundation-independent. I.e., it does not rely on a specific basic language, reasoning system or make any foundation assumptions about the world. Instead, it introduces several concepts to maximize modularity and to abstract from and mediate between different foundations, to reuse concepts, tools, and formalizations. The OMDoc/MMT language integrates successful representational paradigms

• the logics-as-theories representation from logical frameworks,
• theories and the reuse along theory morphisms from object-oriented modeling,
• the Curry-Howard correspondence from type theoretical foundations,
• URIs as globally unique logical identifiers from OpenMath,
• the standardized XML-based interchange syntax of OMDoc,

and makes them available in a single, coherent representational system for the first time. The combination of these features is based on a small set of carefully chosen, orthogonal primitives in order to obtain a simple and extensible language design. These primitives are

1. constants with optional types and definitions,
2. types and definitions of constants are objects, which are syntax trees with binding, using previously defined constants as leaves,
3. theories, which are lists of constant declarations and
4. theory morphisms, that map declarations in a domain theory to expressions of a target theory.

Using these primitives, logical frameworks, logics and theories within some logic are all uniformly represented as OMDoc/MMT theories, rendering all of those equally accessible, reusable and extendable. Constants, functions, symbols, theorems, axioms, proof rules etc. are all represented as constant declarations, and all terms which are built up from those are represented as objects.

Theory morphisms represent truth-preserving maps between theories. Examples include theory inclusions, translations/isomorphisms between (sub)theories and models/instantiations (by mapping axioms to theorems that hold within a model), as well as a particular theory inclusion called meta-theory, that relates a theory to a theory on a higher level on which it depends. This includes the relation between some low-level theory (such as the theory of the legal domain, the world, or the facts of a legal case) to its underlying foundation (such as first-order logic), and the latter’s relation to the logical framework used to define it – e.g. LF³¹.

All of this naturally gives us the notion of a theory graph, which relates theories (represented as nodes) via vertices representing theory morphisms (as in Figure 1), being right at the design core of the OMDoc/MMT language. It is a central advantage of the OMDoc/MMT system that theory morphisms “transport axioms, definitions, theorems, ... ” to new contexts and thus induce knowledge that is not explicitly represented in the graph. Therefore, it is a central design invariant of the system that we can name all induced objects with canonical URIs, the MMT URIs, which contain enough information to reconstruct the induced objects themselves – given the graph.

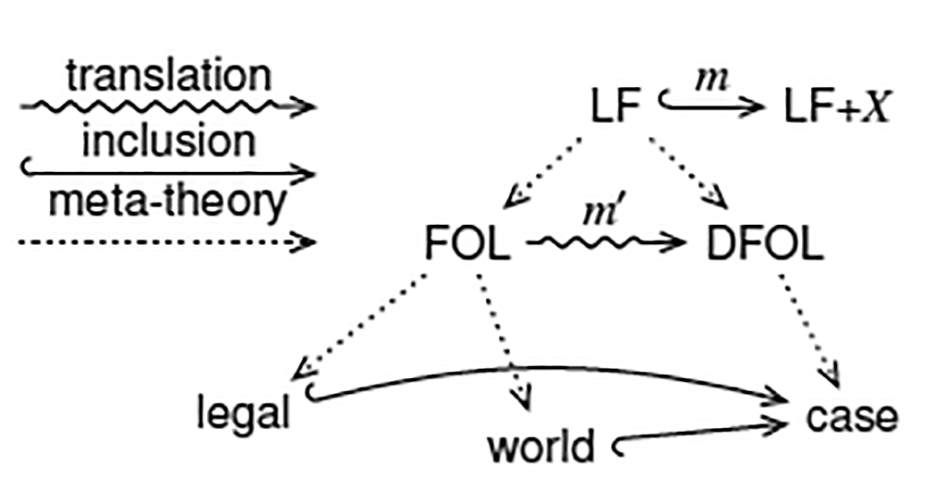
Figure 1: Theory Graph with Meta-Theories

In this setting, meaning trickles down from the urtheories – the only ones that need to be directly implemented in the underlying MMT system – via the logics to the domain level. This gives us a choice of foundations – e.g. between first-order logic (FOL) for descriptions of the world and a defeasible logic (DFOL) for arguing about the facts of a case. MMT comes with a large atlas ³² with hundreds of classical and non-classical logics modularly represented as MMT meta-theories.

One of the salient features of MMT we exploit for context graphs is that theories and morphisms form a category with co-limits, and that MMT can compute pushouts automatically. In a pushout, the situation is as shown on the right: An inclusion P ↪ C and a view P ⇝ S together induce the pushout S ↪ V ⇜ C. We call configurations P ↪ B functors as they can be “applied” to an argument theory A over an application view P ⇝ A. We indicate pushout constructions in diagram by placing a pushout symbol into the commuting square pointing to the computed result theory V. Pushouts give us a very structured way of encoding knowledge application in diagrams. As we use the propositions-as-types encoding of assertions, the application views naturally encode the proof obligations that encode the applicability of the functor.

Context graphs are a subcategory of theory graphs in which the theories are internally consistent theories of some base logic. They can be interpreted as belief sets or possible worlds. In context graphs we model legal syllogisms involving subsumption as pushouts: the functor corresponds to the major premise of the syllogism: it consists of a theory of legal conditions and a theory of legal consequences. The minor premise is modelled as the view v: it proves that all conditions from P are instantiated by the subsumed theory S. If this is the case, then the legal consequences – as instantiated via v follow and are added to the graph as a new theory V.

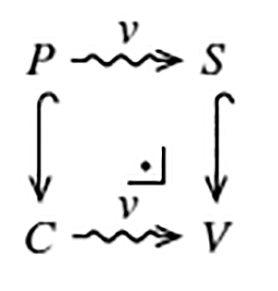
In addition, context graphs are equipped with a defined theory relation called attack. Attacks can be defined in terms of diagrams consisting of theories, views and certain features of the base logic. As such they require no additional expansion of the framework³³.

Finally, an important MMT-feature for our purposes is the theories-as-types approach. This enables to convert theories into types that in turn can be assigned to constants as they appear within in theories.³⁴ In this way legal concepts can be nested within each other and expanded as needed.

Consider the following scheme of legal syllogism:

1. Major Premise (“Obersatz”): A is defined in terms of B₁, . . . , B_n;
2. Minor Premise (“Untersatz”): C satisfies B₁, . . . , B_n;
3. Conclusion (“Schlussatz”): C is an instance of A.

This scheme is used in law application/subsumption to arrive at legal decisions. We model it using analogical reasoning. As such it is not merely a logical inference rule. Rather, its susbsumtion component is to be modelled as with an inference algorithm that extends the context graph as needed. It consists of three components:

• A logical inference system operating on legal propositions formalized in the base logic.
• An analogical inference system operating on contexts/theories.
• An argumentative inference system operating on legal arguments, i.e., sequences of logical and analogical inferences.

The logical inference system is deductive and analytic. Its derivations are strict proofs. The analogical inference system is ampliative and defeasible: it adds new subsumption rules (and attacks) in the form of views to the context graph and uses them to “push out” the coverage of a given major premise to a new domain. It uses heuristics to find view candidates and then calls the logical inference system to discharge any proof obligations that arise. In this way the view serves a guide to compute those parts of the logical closure that are needed to establish subsumption of the theory to be subsumed. Thus, the combination of the two systems yields defeasible arguments in favor of (or against) subsuming one context under another.

The strength of the argument in favor of the new subsumption determines whether the addition to the knowledge base and hence the syllogism application succeeds. This determination in turn requires the construction of syllogistic arguments for and against the subsumption rule candidate, yielding a recursive process that terminates once it reaches “ground truth”, i.e., a syllogism that proceeds purely deductively from premises and existing subsumption rules.

Finally, the argumentative system enforces consistency: whenever the logical and analogical inference systems together allow the derivation of conflicting results it forces a decision for one of the options.

The logical inference system is obtained through automatic or interactive prover support for the respective base logic. Extending MMT with such prover support is ongoing work. The analogical inference system is based on the view finder presented in Müller et al. (2018)³⁵ . It would need to be extended by powerful heuristic and possibly subsymbolic methods to generate more complicated subsumption candidates. As attack is a relation defined in terms of views, the same view finding techniques can also be applied to find attacks. Finally, the argumentation component is based on the usual abstract argumentation semantics ³⁶.

All of the inference systems may in principle be undecidable: not every logical consequence of the propositions may be inferable by the logical inference system; the analogical inference system – being ampliative – is necessarily undecidable; finally, the argumentative system may not be able to find all attack relations between arguments.

This being said, the systems are sound in the following sense: every logical derivation found or certified by the system is correct; every subsumption found or certified by the system is syntactically correct; thus, every argument found or certified by the system is a correct legal argument. Finally, every attack between arguments found or certified by the system is a correct attack.

We will illustrate our approach by using the following legal practice problem as an example. Even though it is very simple – it is one of the first problems budding legal students are given to sharpen their legal reasoning skills – it already shows many legal complexities.

Taschengeldfall: Der 16-jährige Fabian hat wegen einer längeren Krankheit sein wöchentliches Taschengeld nich ausgeben können und daher 50€ angespart. Da er nichts von „Anlegen für schlechte Tage“ hält, will der das Geld sofort ausgeben. Im Spielwarengeschäft des M entdeckt er eine täuschend echt aussehende Spielzeugpistole, mit der er seinen Freunden mal so richtig „einheizen“ will. Auf Nachfrage des M teilt F diesem mit, dass er die Pistole von seinem Taschengeld kaufe und dass seine Eltern hiermit auch einverstanden seien. Dabei hatten F’s Eltern diesem explizit verboten „solchen Unfug“ zu kaufen. Waffen, wenn auch nur Spielzeugwaffen, hätten in ihrem Haus nichts zu suchen. Die gekaufte Pistole versteckte F in seinem Zimmer, wo sie seine Mutte sehr zu ihrem Missfallen am nächsten Tag fand. F’s Eltern verlange von M die Rückerstattung des Kaufpreises gegen Rückgabe der Pistole. Dies lehnt M ab. Immerhin hätte die Pistole ja deutliche Gebrauchsspuren.

Bearbeitungsvermerk: Er ist davon auszugehen, dass M das Geld noch hat und gesondert aufbewahrt. Frage: Kann F – vertreten durch seine Eltern – von M Rückzahlung des Kaufpreises gegen Rückgabe der Pistole verlangen?

This little “case” has two possible solutions: one argues via §985 BGB (claim to return possession of the bills/money, which is still owned by the minor F) and another via §812 Alt. 1 BGB (claim to pay back the purchase price); both conclude that M needs to recompense F. A schematic visualization of the structure of the first argument is given on the left of Figure 2. On the right we show an OMDoc/MMT theory graph that implements the same structural intuitions in an MMT context applying the method put forward Rapp et al (2020)³⁷ to the allowance case. Figure 2b thus could be the result of an application of the intended inference system to the allowance case.

Procedurally, we expect that an inference algorithm would follow the nesting in Figure 2a. Hence it starts with the “facts”-theory in the right upper corner of Figure 2b. The analogical system is called to find subsumption candidates in the existing context graph formalization of the law. E.g., in this case it might find §985 (the two boxes below the facts theory; technically, we have to first apply a temporal default rule). §985 requires an owner which is instantiated by the boy Fabian in this example. However, that subsumption itself has to be justified which is again done through the construction of syllogistic arguments for and against. Arguments for proceed by discharging the proof obligations of the subsumption candidate through the logical system and elaborating the predicate (or type) “Eigentümer” to its corresponding theory, in turn mapping its declarations to the facts and so forth.

Thus the reasoning process moves in the manner of definition unpacking until either further proof or view finding fails or all proof obligations can be discharged. Some boxes can be evaluated “lazily”, e.g. the statute of limitations (Anspruch erloschen?) may have a default value and may only need to be checked in reaction to a challenge (burden of proof).

An argument against the application of §985 can be constructed from §929 which states that the original owner of the money loses his property in it if he transfered it in a valid transfer agreement. Hence if F entered in a valid transfer agreement, he cannot be the owner of the money anymore. At this level, further conflicting subsumption candidates arise: on one side it can be argued that the declaration of intent (Willenserklärung) of the minor is valid because his intention (§110) or the legitimitate expectation of the seller should be legally relevant or it is invalid because the objection of the minor’s parents (to his purchase of the toy gun) should take legal priority (§§106, 107 and Article 6 GG). In fact, the parents win in this case due to Article 6 GG: they can mandate how the son can use his allowance. Hence the outcome of this argumentation process (which is collapsed in Figure 2b) is an attack on the application of §929.

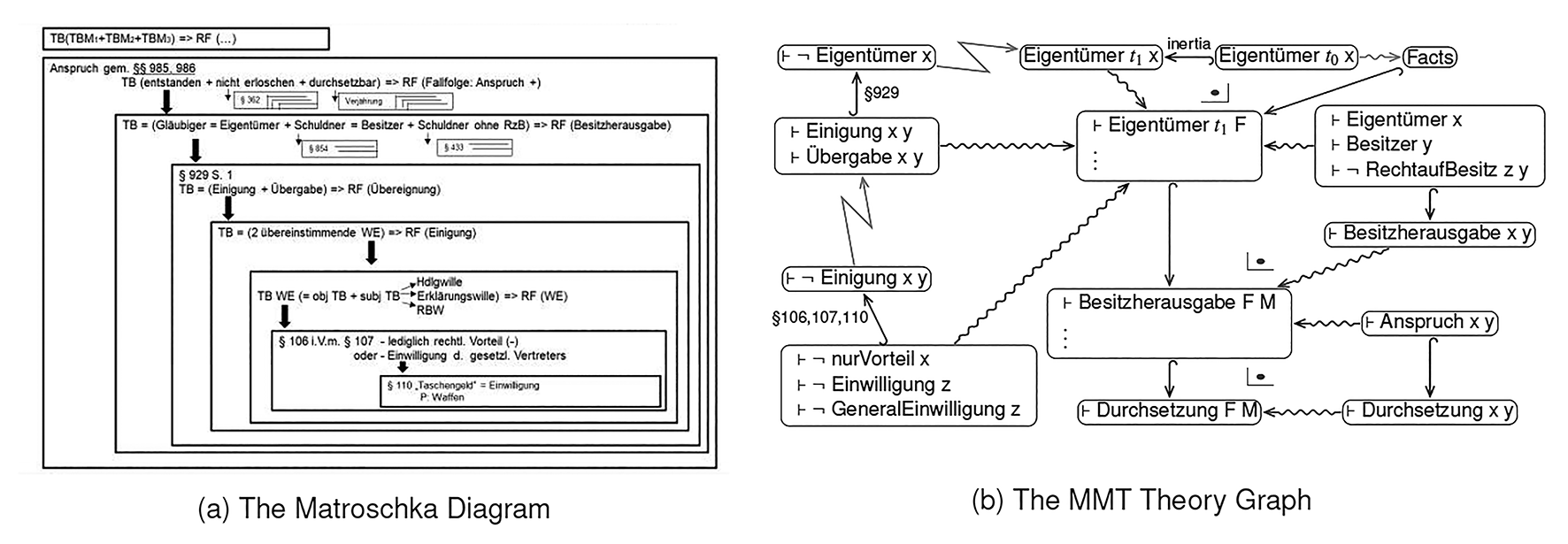
Figure 2: Analysis of a case in terms of nested subsumtions of norms

Thus the initial rule application stands and F indeed remained the owner of the money. After this there are two further functor applications to the thusly modified facts, eventually yielding the result that F has an actionable claim to M. The further details pertaining to checking whether F claim may have expired are ommitted from this diagram for simplicity.

In prior work we have presented a system to represent and check analogical and argumentative reasoning. Here we presented a road map towards extending this towards inference. We have presented an outline of an ampliative, analogical inference algorithm on context-graph-based representations of legal knowledge. Implementing this algorithm will require work on two fronts: firstly, careful fine tuning of the representation formalism to ensure powerful yet decidable logical and type inference wherever possible. Secondly, building on our existing work on view finding to enable the analogical inference component of the system. Currently, views can only be found if they don’t require theorem proving. In the future we want to use prover integration to find more complex views and thereby subsumption candidates and attacks. Indeed, it may even be possible to leverage the prover as a reward component in a reinforcement learning system that is trained to find view candidates. The prover would attempt to verify the candidates generated by the learner and provide positive feedback if this succeeds.

• F. Rabe and M. Kohlhase, “A Scalable Module System”. In: Information & Computation 0.230, 2013, pp. 1–54. url: https://kwarc. info/frabe/Research/mmt.pdf. Monographs.
   
• D. Müller, M. Kohlhase, and F. Rabe, “Automatically Finding Theory Morphisms for Knowledge Management”. In: Intelligent Computer Mathematics. Ed. by F. Rabe, W. M. Farmer, G. O. Passmore, and A. Youssef. LNAI 11006. Springer, 2018. doi: 10.1007/978-3- 319-96812-4.
   
• K. Atkinson and T. Bench-Capon, “Reasoning with Legal Cases: Analogy or Rule Application?” In: Proceedings of the Seventeenth International Conference on Artificial Intelligence and Law. ICAIL ’19. Association for Computing Machinery, 2019, pp. 12–21. doi: 10.1145/3322640.3326695.
   
• L. M. Al-Abdulkarim, “A Methodology for Designing Systems to Reason with Legal Cases using Abstract Dialectical Frameworks”. In: Artificial Intelligence and Law 24.1, 2016, pp. 1–49.
   
• V. A. W. M. M. Aleven, “Teaching Case-Based Argumentation through a Model and Examples”, PhD thesis, University of Pittsburgh, 1997.
   
• K. Ashley, Artificial Intelligence and Legal Analytics, Cambrige University Press, 2017.
   
• K. D. Ashley, Modeling Legal Argument. Reasoning with Cases and Hypotheticals. Artificial intelligence and legal reasoning,. MIT Press, 1990.
   
• P. Bartha, By Parallel Reasoning, Oxford University Press, 2010.
   
• P. Bartha, “Analogy and Analogical Reasoning”. In: The Stanford Encyclopedia of Philosophy. Ed. by E. N. Zalta. Spring 2019, Metaphysics Research Lab, Stanford University, 2019.
   
• T. Bench-Capon, “Representing Popov v Hayashi with dimensions and factors”. In: Artificial Intelligence and Law 20.1, 2012, pp. 15–35. doi: 10.1007/s10506-012-9118-7.
   
• BENCH-CAPON. The Need for Good Old-fashioned AI and Law. In W. Hotzendorfer, C. Tschohl and F. Kummer (Hrsg.) International Trends in Legal Informatics: A Festschrift for Erich Schweighofer. Editions Weblaw: Bern. Pages 23-36, 2020.
   
• Bondarenko, P. Dung, R. Kowalski and F. Toni “An abstract, argumentation-theoretic approach to default reasoning”. In: Artificial Intelligence 93.1, 1997, pp. 63–101. doi: 10.1016/S0004-3702(97)00015-5.
   
• M. Codescu, F. Horozal, M. Kohlhase, T. Mossakowski and F. Rabe, “Project Abstract: Logic Atlas and Integrator (LATIN)”. In: Intelligent Computer Mathematics, Ed. by J. Davenport, W. Farmer, F. Rabe, and J. Urban, LNAI 6824, Springer Verlag, 2011, pp. 289–291, url: www.gl.mathhub.info/MMT/LATIN; LATIN2 – Logic Atlas Version 2. url: www.gl.mathhub.info/MMT/LATIN2.
   
• T. R. Davies and S. J. Russell, “A Logical Approach to Reasoning by Analogy”. In: Proceedings of the 10th International Joint Conference on Artificial Intelligence – Volume 1, IJCAI’87, Milan, Italy: Morgan Kaufmann Publishers Inc., 1987, pp. 264–270.
   
• Dung, On the acceptability of arguments and its fundamental role in nonmonotonic reasoning, logic programming, and n–person games. Artificial Intelligence. 77 (2): 321–357.
   
• B. Falkenhainer, K. D. Forbus, and D. Gentner, “The structure-mapping engine: Algorithm and examples”. In: Artificial Intelligence 41.1, 1989, pp. 1–63. doi: 10.1016/0004-3702(89)90077-5.
   
• K. D. Forbus, R. W. Ferguson, A. Lovett and D. Gentner, “Extending SME to Handle Large-Scale Cognitive Modeling”. In: Cognitive Science 41.5, 2017, pp. 1152–1201. doi: 10.1111/cogs.12377.
   
• T. F. Gordon and D. Walton, “The Carneades Argumentation FrameworkUsing Presumptions and Exceptions to Model Critical Questions”. In: Proceedings of the 2006 Conference on Computational Models of Argument: Proceedings of COMMA 2006, NLD: IOS Press, 2006, pp. 195–207.
   
• H. L. A. Hart, The Concept of Law, 3rd ed., Oxford University Press, 2012.
   
• M. Hesse, Models and Analogies in Science, University of Notre Dame Press, 1966.
   
• J. E. Hummel and K. J. Holyoak, “A symbolic-connectionist theory of relational inference and generalization.” In: Psychological review 110 2, 2003, pp. 220–64.
   
• F. Horozal, M. Kohlhase and F. Rabe, “Extending MKM Formats at the Statement Level”. In: Intelligent Computer Mathematics, Ed. by J. Jeuring, J. A. Campbell, J. Carette, G. Dos Reis, P. Sojka, M. Wenzel, and V. Sorge, LNAI 7362, Berlin and Heidelberg, Springer Verlag, 2012, pp. 65–80. url: https://kwarc.info/kohlhase/papers/mkm12-p2s.pdf.
   
• K. J. Holyoak and P. Thagard, “Analogical mapping by constraint satisfaction”. In: Cognitive Science 13.3, 1989, pp. 295–355,
  url: http://www.sciencedirect.com/science/article/pii/0364021389900165.
   
• M. Kohlhase and M. Iancu, “Co-Representing Structure and Meaning of Mathematical Documents”. In: Sprache und Datenverarbeitung, International Journal for Language Data Processing 38.2, 2014, Special Issue “The language of mathematics – computational, linguistic and logical aspects”, pp. 49–80. url: https://kwarc.info/kohlhase/papers/omdoc-semantics.pdf.
   
• M. Kohlhase, “A Data Model and Encoding for a Semantic, Multilingual Terminology of Mathematics”. In: Intelligent Computer Mathematics. Ed. by S. Watt, J. Davenport, A. Sexton, P. Sojka, and J. Urban, LNCS 8543, Springer, 2014, pp. 169–183. url: https://kwarc.info/kohlhase/papers/cicm14-smglom.pdf.
   
• M. Mitchell, Analogy-making as perception: A computer model, Mit Press, 1993.
   
• J. D. Norton, The Material Theory of Induction, 2020.
  url: http://www.pitt.edu/~jdnorton/papers/material_theory/Material_Induction_Apr_24_2020.pdf.
   
• F. Pfenning, “Logical Frameworks”. In: Handbook of Automated Reasoning, Ed. by A. Robinson and A. Voronkov, Vol. I and II, Elsevier Science and MIT Press, 2001.
   
• H. Prakken and S. Modgil, “The ASPIC+ Framework for Structured Argumentation: a Tutorial”. In: Argument and Computation 5.1, 2014, pp. 31–62.
   
• H. Prakken, “Reconstructing Popov v. Hayashi in a Framework for Argumentation with Structured Arguments and Dungean Semantics”. In: Artificial Intelligence and Law 20.1, 2012, pp. 57–82.
   
• F. Rabe, “How to Identify, Translate, and Combine Logics?” In: Journal of Logic and Computation 27.6, 2017, pp. 1753–1798.
   
• Ranta, Grammatical Framework: Programming with Multilingual Grammars, CSLI Publications, 2011.
   
• Rapp, Adrian and Kohlhase, Context Graphs for Legal Reasoning and Argumentation, Proceedings of the Third International Workshop on Systems and Algorithms for Formal Argumentation co-located with the 8th International Conference on Computational Models of Argument (COMMA), 2020, p. 56–67.
   
• D. Schlimm, “Two Ways of Analogy: Extending the Study of Analogies to Mathematical Domains”. In: Philosophy of Science 75.2, 2008, pp. 178–200. doi: 10.1086/590198.
   
• J. F. Sowa and A. K. Majumdar, “Analogical reasoning”. In: International Conference on Conceptual Structures, Springer, 2003, pp. 16–36.
   
• C. Sacerdoti Coen and E. Tassi, The ELPI system, 2015. url: https://github.com/LPCIC/elpi.
   
• K. Stevens, “Reasoning by Precedent – Between Rules and Analogies”. In: Legal Theory 24.3, 2018, pp. 216–254.